
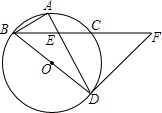
 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.分析 (1)由圆周角定理可知:∠BDA=∠ABE,从而可证明:△ABE∽△ADB;
(2)由(1)可知:AB2=AE•AD,从而可求出AB的长度,由圆周定理可知:∠BAD=90°,所以tan∠ADB=$\frac{AB}{AD}$=2$\sqrt{3}$.
(3)连接CD,由(2)可知∠ADB=30°,利用勾股定理可知BD=4$\sqrt{3}$,从而可求出CD以及BC的长度,利用三角形面积公式即可求出△BCD的面积,从而可知△CDF的面积,进而求出CF的长度.
解答 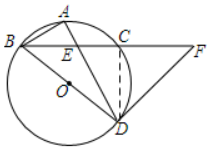 解:(1)∵A是$\widehat{BC}$的中点,
解:(1)∵A是$\widehat{BC}$的中点,
∴$\widehat{BA}=\widehat{AC}$,
∴∠BDA=∠ABE,
∵∠BAE=∠BAE,
∴△ABE∽△ADB,
(2)由(1)可知:$\frac{AE}{AB}$=$\frac{AB}{AD}$,
∴AB2=AE•AD,
∵AE=2,ED=4.
∴AB=2$\sqrt{3}$,
∵BD是⊙O的直径,
∴∠BAD=90°,
∴tan∠ADB=$\frac{AB}{AD}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$;
(3)连接CD,
∵AB=2$\sqrt{3}$,AD=6,
∴由勾股定理可知:BD=4$\sqrt{3}$,
由(2)可知:tan∠ADB=$\frac{\sqrt{3}}{3}$
∴∠ADB=30°,
∴∠ABE=∠ADB=30°,
∴∠DBC=30°,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴sin∠DBC=$\frac{CD}{BD}$,
∴CD=2$\sqrt{3}$,
由勾股定理可知:BC=6,
∴S△BDC=$\frac{1}{2}$BC•CD=6$\sqrt{3}$,
∴S△CDF=S△BDF-S△BDC=2$\sqrt{3}$,
∵S△CDF=$\frac{1}{2}$CF•CD,
∴CF=2,
∴tan∠F=$\frac{CD}{CF}$=$\sqrt{3}$,
∴∠F=60°,
∴∠BDF=90°,
∴DF与⊙O相切.
点评 本题考查圆的综合问题,涉及圆周角定理,相似三角形的判定与性质,勾股定理三角形面积公式,特殊角的三角函数等知识,综合程度较高.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10×108 | B. | 0.1×1010 | C. | 1×109 | D. | 1×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校举行“文明环保,从我做起”征文比赛.现有甲班上交40篇作文,乙班上交30篇作文,现将两班的作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲班上交40篇作文,乙班上交30篇作文,现将两班的作文的成绩(单位:分)统计如下:| 等级 | 成绩(S) | 频数 |
| A | 90<S≤100 | x |
| B | 80<S≤90 | 16 |
| C | 70<S≤80 | 18 |
| D | S≤70 | 3 |
| 合计 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com