
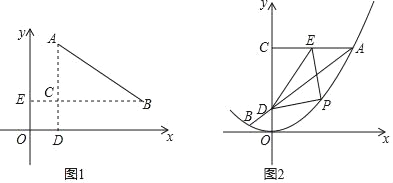
【题目】(1)如图1,若点A坐标为(x1,y1),点B坐标为(x2,y2),作AD⊥x轴于点D,BE⊥y轴于点E,AD与BE相交于点C,则有AC=|y1﹣y2|,BC=|x1﹣x2|,所以,A、B两点间的距离为AB=![]() .
.
根据结论,若M、N两点坐标分别为(1,4)、(5,1),则MN= (直接写出结果).
(2)如图2,直线y=kx+1与y轴相交于点D,与抛物线y=![]() x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
①a= ,k= ,AD= (直接写出结果).
②若△DEP是以DE为底的等腰三角形,求点P的横坐标;
③求四边形CDPE的周长的最小值.
【答案】(1)5(2)①4,![]() ,5②
,5②![]() ③5+
③5+![]()
【解析】
(1)利用题目提供的两点间距离公式即可求解;
(2)①将点A的坐标代入二次函数表达式得:a=![]() ×42=4,则点A坐标为(4,4),将点A的坐标代入一次函数表达式得k=
×42=4,则点A坐标为(4,4),将点A的坐标代入一次函数表达式得k=![]() ,即可求解;
,即可求解;
②利用PD=PE,整理得:3x2+8x﹣38=0,即可求解;
③在y轴上,截取CD′=CD,连接D′E并延长交抛物线于点P,则此时,四边形CDPE的周长最小,最小值=CD+CE+PD′=5+PD′,即可求解.
(1)MN=![]() =5,
=5,
故答案为5;
(2)①将点A的坐标代入二次函数表达式得:a=![]() ×42=4,则点A坐标为(4,4),点E的坐标为(2,4),
×42=4,则点A坐标为(4,4),点E的坐标为(2,4),
将点A的坐标代入一次函数表达式得:4=4k+1,解得k=![]() ,
,
∵CD=3,CE=4,
∴AD=5,
故:答案为:4,![]() ,5;
,5;
②设点P的横坐标为x,即点P坐标为(x,![]() x2),点D、E的坐标分别为(0,1)、(2,4),
x2),点D、E的坐标分别为(0,1)、(2,4),
由题意得:PD=PE,即:PD2=PE2,
x2+![]() =(x﹣2)2+(
=(x﹣2)2+(![]() x2﹣4)2,整理得:3x2+8x﹣38=0,
x2﹣4)2,整理得:3x2+8x﹣38=0,
解得:x=![]() (负值已舍去),
(负值已舍去),
即点P的横坐标为![]() ;
;
③在y轴上,截取CD′=CD,连接D′E并延长交抛物线于点P,则此时,四边形CDPE的周长最小,
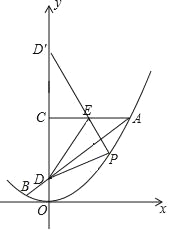
DE+PE=PD′,点D′的坐标为(7,0),
四边形CDPE的周长最小值=CD+CE+PD′=5+PD′,
直线D′E的表达式为:y=kx+7,把点E的坐标代入上式得:4=2k+7,解得:k=﹣![]() ,
,
则直线D′E的表达式为:y=﹣![]() x+7,
x+7,
将该表达式与二次函数表达式联立并求解得:x=![]() ﹣3,即点P的坐标为(
﹣3,即点P的坐标为(![]() ﹣3,
﹣3,![]() ),
),
则PD′=![]() =
=![]() ,
,
四边形CDPE的周长最小值=5+![]() .
.
故答案为:(1)5(2)①4,![]() ,5②
,5②![]() ③5+
③5+![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
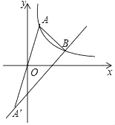
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1=![]() (x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(1)设a=2,点B(4,2)在函数y1,y2的图象上.
①分别求函数y1,y2的表达式;
②直接写出使y1>y2>0成立的x的范围.
(2)如图,设函数y1,y2的图象相交于点B,点B的横坐标为3a,△AA′B的面积为16,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】举世瞩目的港珠澳大桥已于2018年10月24日正式通车,这座大桥是世界上最长的跨海大桥,被英国《卫报》誉为“新世界七大奇迹”,车辆经过这座大桥收费站时,从已开放的4个收费通道A、B、C、D中可随机选择其中一个通过.
(1)一辆车经过收费站时,选择A通道通过的概率是 .
(2)用树状图或列表法求两辆车经过此收费站时,选择不同通道通过的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
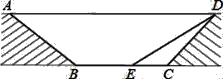
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.
(1)求第10场比赛的得分;
(2)直接写出这10场比赛的中位数,众数和方差.
方差公式:s2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
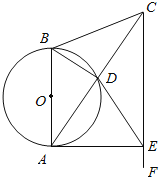
A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连接PN、MQ.
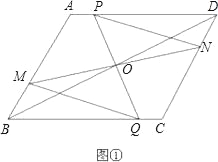

(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在图②所示的位置,画出图形,证明你的猜想;
(3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com