
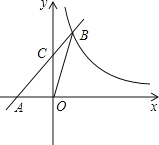
【题目】如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=![]() 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<
在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<![]() 的解集是0<x<1.其中正确的有( )
的解集是0<x<1.其中正确的有( )
A.0个B.1个C.2个D.3个
【答案】A
【解析】
①将y=0代入y=x+2中求出x值,由此即可得出OA的长度,结合点B的纵坐标结合三角形的面积即可求出S△AOB=3,结论①不正确;②当x1>0>x2时,可得出y1>0>y2,结论②不正确;③联立两函数解析式成方程组,解方程组可得出两函数图象的交点坐标,根据两函数图象的上下位置关系结合图形即可得出不等式x+2<![]() 的解集是x<-3或0<x<1,结论③不正确.综上即可得出结论.
的解集是x<-3或0<x<1,结论③不正确.综上即可得出结论.
①当y=x+2=0时,x=﹣2,
∴点A(﹣2,0),
∴OA=2,
∴S△AOB=![]() OA|yB|=
OA|yB|= ![]() ×2×3=3,结论①不正确;
×2×3=3,结论①不正确;
②当x1>0>x2时,y1>0>y2,结论②不正确;
③联立两函数解析式成方程组,
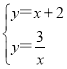 ,解得:
,解得: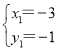 ,
,![]() ,
,
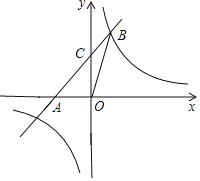
观察函数图象可知:当x<﹣3或0<x<1时,直线y=x+2在反比例函数y=![]() 图象的下方,
图象的下方,
∴不等式x+2<![]() 的解集是x<﹣3或0<x<1,结论③不正确.
的解集是x<﹣3或0<x<1,结论③不正确.
故选:A.


科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设D,E,F依次是△ABC的三边AB,BC,CA或其延长线上的点,且这三点共线,则满足![]() .
.
这个定理的证明步骤如下:
情况①:如图1,直线DE交△ABC的边AB于点D,交边AC于点F,交边BC的延长线与点E.
过点C作CM∥DE交AB于点M,则![]() ,
,![]() (依据),
(依据),
∴![]() =
=![]() ,
,
∴BEADFC=BDAFEC,即![]() .
.
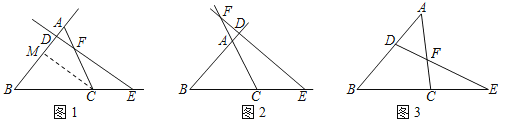
情况②:如图2,直线DE分别交△ABC的边BA,BC,CA的延长线于点D,E,F.
…
(1)情况①中的依据指: ;
(2)请你根据情况①的证明思路完成情况②的证明;
(3)如图3,D,F分别是△ABC的边AB,AC上的点,且AD:DB=CF:FA=2:3,连接DF并延长,交BC的延长线于点E,那么BE:CE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
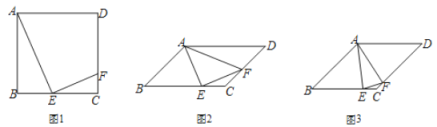
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F.
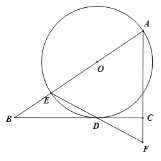
(1)求证:AE=AF;
(2)若BC=4,AC=3,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提倡节约用电,某地区规定每月用电量不超过 a 千瓦·时,居民生活用电基本价格为每千瓦时 0.5 元;若每月用电量超过 a 千瓦·时,则超过部分按基本电价提高 20%收费.居住此地的老李家二月份用电 120 千瓦·时,所交的电费为 66 元.
(1)求 a 的值;
(2)老李登录当地国家电网网络平台缴费后弹出一个对话框:您的家庭一月份和二月份的平均电费不超过0.54 元/千瓦·时,评为“节能小家庭”.试计算老李家一月份的用电量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
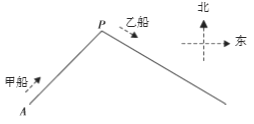
【题目】小岛![]() 在港口
在港口![]() 的南偏西45°方向,距离港口81海里处.甲船从
的南偏西45°方向,距离港口81海里处.甲船从![]() 出发,沿
出发,沿![]() 方向以6海里/时的速度驶向港口,乙船从港口
方向以6海里/时的速度驶向港口,乙船从港口![]() 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
(1)出发后 小时两船与港口![]() 的距离相等;
的距离相等;
(2)出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
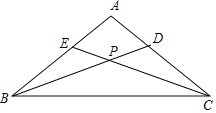
【题目】如图,在等腰△ABC中,AB=AC,CE、BD分别为∠ACB、∠ABC的角平分线,CE、BD相交于P.
(1)求证:CD=BE;
(2)若∠A=98°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
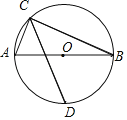
【题目】如图,AB是⊙O的直径,点C是⊙O上一点(点C不与A,B重合),连接CA,CB.∠ACB的平分线CD与⊙O交于点D.
(1)求∠ACD的度数;
(2)探究CA,CB,CD三者之间的等量关系,并证明;
(3)E为⊙O外一点,满足ED=BD,AB=5,AE=3,若点P为AE中点,求PO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com