
 如图,已知AB∥A′B′,BC∥B′C′,那么下列比例式成立的是( )
如图,已知AB∥A′B′,BC∥B′C′,那么下列比例式成立的是( )| A. | $\frac{OA′}{OA}$=$\frac{OC}{OC′}$ | B. | $\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$ | C. | $\frac{A′C′}{AC}$=$\frac{OC}{OC′}$ | D. | $\frac{AB}{A′B′}$=$\frac{OC′}{OC}$ |
分析 由AB∥A′B′,BC∥B′C′,根据平行线分线段成比例定理,即可求得答案.
解答 解:∵AB∥A′B′,
∴$\frac{OA}{OA′}$=$\frac{OB}{OB′}$=$\frac{AB}{A′B′}$,
∵BC∥B′C′,
∴$\frac{OB}{OB′}$=$\frac{OC}{OC′}$=$\frac{BC}{B′C′}$,
∴$\frac{OA}{OA′}$=$\frac{OB}{OB′}$=$\frac{AB}{A′B′}$=$\frac{OC}{OC′}$=$\frac{BC}{B′C′}$,
∴$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$.
故选B.
点评 本题考查了平行线分线段成比例定理,解题的关键是利用平行线得到比例式,注意相等的比例式的代换.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:填空题
 如图,⊙O的直径AB=2,P是上半圆(A、B除外)上任一点,∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,则EF的长是$\sqrt{3}$.
如图,⊙O的直径AB=2,P是上半圆(A、B除外)上任一点,∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,则EF的长是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| X | -1 | 0 | 1 | 3 |
| y | -$\frac{13}{5}$ | 3 | $\frac{29}{5}$ | 3 |
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
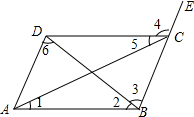 如图根据图形填空:
如图根据图形填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小杰同学研究两平行线被第三条直线所截构成的同位角、内错角、同旁内角的角平分线的位置关系发现了一些比较特殊,你也有同样的发现吗?
小杰同学研究两平行线被第三条直线所截构成的同位角、内错角、同旁内角的角平分线的位置关系发现了一些比较特殊,你也有同样的发现吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,一次函数y=x+m的图象与反比例函数y=-$\frac{3}{2x}$的图象交于A、B两点,A点坐标为(1,n),连接OB,过点B作BC⊥x轴,垂足为C.
已知,如图,一次函数y=x+m的图象与反比例函数y=-$\frac{3}{2x}$的图象交于A、B两点,A点坐标为(1,n),连接OB,过点B作BC⊥x轴,垂足为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com