
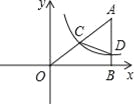
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
【答案】y=![]() ;
; ![]()
【解析】试题分析:(1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=![]() 中,即可确定反比例函数解析式;
中,即可确定反比例函数解析式;
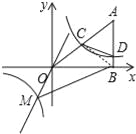
(2)先将y=3x与y=![]() 联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
试题解析:(1)∵A点的坐标为(8,y),∴OB=8,∵AB⊥x轴于点B,sin∠OAB=![]() ,
,
∴![]() ,∴OA=10,由勾股定理得:AB=
,∴OA=10,由勾股定理得:AB=![]() ,
,
∵点C是OA的中点,且在第一象限内,∴C(4,3),∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=12,∴反比例函数解析式为:y=![]() ;
;
(2)将y=3x与y=![]() 联立成方程组,得:
联立成方程组,得: 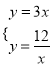 ,
,
解得: ![]() ,
, ![]() ,
,
∵M是直线与双曲线另一支的交点,∴M(﹣2,﹣6),∵点D在AB上,∴点D的横坐标为8,
∵点D在反比例函数y=![]() 的图象上,∴点D的纵坐标为
的图象上,∴点D的纵坐标为![]() ,∴D(8,
,∴D(8,![]() ),∴BD=
),∴BD=![]() ,
,
连接BC,如图所示,∵S△MOB=![]() 8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=
8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=![]() 83+
83+![]() =15,
=15,
∴![]() .
.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
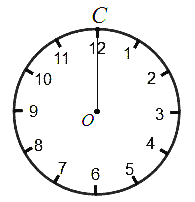
【题目】钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点![]() 为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径
为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径![]() 表示时针,半径
表示时针,半径![]() 表示分针,它们所成的钟面角为∠
表示分针,它们所成的钟面角为∠![]() ;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.
;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.
(1)时针每分钟转动的角度为 °,分针每分钟转动的角度为 °;
(2)8点整,钟面角∠![]() = °,钟面角与此相等的整点还有: 点;
= °,钟面角与此相等的整点还有: 点;
(3)如图,设半径![]() 指向12点方向,在图中画出6点15分时半径
指向12点方向,在图中画出6点15分时半径![]() 、
、![]() 的大概位置,并求出此时∠
的大概位置,并求出此时∠![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
成 绩 | 45 | 46 | 47 | 48 | 49 | 50 |
人 数 | 1 | 2 | 4 | 2 | 5 | 1 |
这此测试成绩的中位数和众数分别为( )
A.47, 49
B.48, 49
C.47.5, 49
D.48, 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从![]() 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:
加数的个数 | 连续奇数的和 |
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )当
)当![]() 的值为__________.
的值为__________.
(![]() )用含
)用含![]() 的代数式表示
的代数式表示![]() 个连续奇数之和
个连续奇数之和![]() 的公式,
的公式, ![]() __________.
__________.
用含![]() 的代数式表示从
的代数式表示从![]() 开始的第
开始的第![]() 个连续奇数是__________.
个连续奇数是__________.
(![]() )根据规律计算
)根据规律计算![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF. 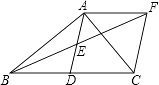
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( ).
A. 等腰三角形一定是锐角三角形
B. 等腰三角形的腰长总大于底边长
C. 等腰三角形的底角的外角一定是钝角
D. 顶角相等的两个等腰三角形是全等三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com