当x= _________ 时，代数式
的值等于﹣2．
新课标阶梯阅读训练系列答案科目：初中数学 来源：新课标教材导学 数学七年级(第一学期) 题型：044
四个连续自然数的积再加上1一定是一个完全平方数．完全平方数是这样一种数：它可以写成一个正整数的平方．例如：16是4的平方，81是9的平方．
我们看下面的例子：
1·2·3·4＋1＝25(＝52)；2·3·4·5＋1＝121(＝112)；
3·4·5·6＋1＝361(＝192)；
如果我们设四个连续自然数中最小的一个是n，那么这四个连续自然数的积加上1的和可以表示为n(n＋1)(n＋2)(n＋3)＋1，它的结果是n2＋3n＋1的平方，因为n为自然数，所以n2＋3n＋1也是一个自然数，即：
n(n＋1)(n＋2)(n＋3)＋1＝(n2＋3n＋1)2．①
学到整式的乘法时，我们还可以证明这个等式成立．
当n取任意自然数代入①，不仅可以知道n(n＋l)(n＋2)(n＋3)＋1是一个完全平方数，还可以知道它是什么数的平方．
你可以算一算：20·21·22·23＋1＝？，50·51·52·53＋1＝？
同学们，根据同样的道理，四个连续偶数(或奇数)的积再加上16是一个完全平方数吗？请你试一试．
查看答案和解析>>
科目：初中数学 来源：新课程学习手册 数学 八年级(下) 配人教课标版 题型：044
| |||||||
查看答案和解析>>
科目：初中数学 来源： 题型：044
阅读材料：
当抛物线的关系式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发生变化．例如：由抛物线y=x2-2mx+m2+2m-1，①
有y=(x-m)2+2m-1. ②
当m的值变化时，x、y的值也随之变化，因而y值也随x值的变化而变化．将③代入④，得y=2x-1 ⑤．可见，不论m取任何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式y=2x-1．
解答问题：（1）在上述过程中，由①到②所用的数学方法是 .其中运用了 公式；由③④得到⑤所用的数学方法是 .
（2）根据阅读材料提供的方法，确定抛物线y=x2-2mx+2m2-3m+1顶点的纵坐标y与横坐标x之间的关系式．
查看答案和解析>>
科目：初中数学 来源：新课程 新理念 新思维·同步练习篇·数学 九年级下册（苏教版） 苏教版 题型：044
阅读理解题．
阅读材料：当抛物线的解析式中含有字母系数时，随着系数中的字母取值的不同，抛物线的顶点坐标也将发生变化．
例如：由抛物线y＝x2－2mx＋m2＋2m－1， ①
有y＝(x－m)2＋2m－1． ②
∴抛物线的顶点坐标为(m，2m－1)，
即
当m的值变化时，x、y的值也随之变化，因而y值也随x值的变化而变化．
将③代入④，得y＝2x－1． ⑤
可见，不论m取任何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式：y＝2x－1．
解答问题：
(1)在上述过程中，由①到②所用的数学方法是________，其中运用了________公式；
由③、④得到⑤所用的数学方法是________．
(2)根据阅读材料提供的方法，确定抛物线y＝x2－2mx＋2m2－3m＋1顶点的纵坐标y横坐标x之间的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
解：（1）A（-1，0），B（3，0），C（0，3）．·················· 2分
抛物线的对称轴是：x=1．······················· 3分
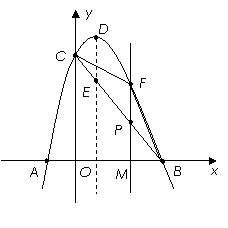（2）①设直线BC的函数关系式为：y=kx+b．
把B（3，0），C（0，3）分别代入得：
解得：k= -1，b=3．
所以直线BC的函数关系式为：
．
当x=1时，y= -1+3=2，∴E（1，2）．
当
时，
，
∴P（m，
m+3）．·························· 4分
在
中，当
时，
∴
当时，
∴
········· 5分
∴线段DE=4-2=2，线段
···· 6分
∵
∴当
时，四边形
为平行四边形．
由
解得：
（不合题意，舍去）．
因此，当
时，四边形为平行四边形．··········· 7分
②设直线
与
轴交于点
，由
可得：
∵
························ 8分
即
．
·········· 9分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=﹣2，
，又因为y＝y1＋y2，
＝