练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小，此时∠MAN的度数为_________°.

    【答案】40

    【解析】

    根据要使△AMN的周长最小，即利用点的对称，使三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M＋∠A″＝∠HAA′＝70°，进而得出∠MAB＋∠NAD＝70°，即可得出答案．

    解：作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，如图：

    ∵∠DAB＝110°，

    ∴∠HAA′＝70°，

    ∴∠AA′M＋∠A″＝∠HAA′＝70°，

    ∵∠MA′A＝∠MAB，∠NAD＝∠A″，

    ∴∠MAB＋∠NAD＝70°，

    ∴∠MAN＝110°70°＝40°，

    故答案为40．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

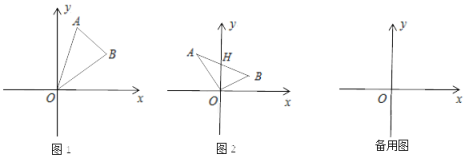
    【题目】在平面直角坐标系中，O为坐标原点，A(m,n+1),B(m+2,n).

    （1）当m=1,n=2时.如图1，连接AB、AO、BO.直接写出△ABO的面积为 .

    （2）如图2，若点A在第二象限、点B在第一象限，连接AB、AO、BO,AB交y轴于H，△ABO的面积为2.求点H的坐标.

    （3）若点A、B在第一象限，在y 轴正半轴上存在点C，使得∠CAB=900,且CA=AB,求m的值，及OC的长（用含n的式子表示）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是矩形的对角线的交点，、、、分别是、、、上的点，且．

    求证：四边形是矩形；

    若、、、分别是、、、的中点，且，，求矩形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成任务。

    筝形的定义:两组邻边分别相等的四边形叫做筝形，几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说，如图，若四边形ABCD是一个筝形，则AB=AD，BC=CD；若AB=AD，BC=CD，则四边形ABCD是筝形.

    如图，四边形ABCD是一个筝形，其中AB=AD，BC=CD.对角线AC，BD相交于点O，过点0作0M⊥AB，ON⊥AD，垂足分别为M，N.求证:四边形AMON是筝形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD＝2, DE＝2,则四边形 OCED 的面积为（　　）

    A. 2 B. 4 C. 4 D. 8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：正方形中，点、、、分别在、、、上，且，

    四边形是正方形吗？为什么？

    若正方形的边长为，且，请求出四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八年级同学到距学校6千米的郊外秋游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往，如图分别表示步行和骑车的同学前往目的地所走的路程y（千米）与所用时间（分钟）之间的函数关系，则以下判断错误的是 （ ）

    A.骑车的同学比步行的同学晚出发30分钟

    B.骑车的同学比步行的同学早6分钟到达目的地

    C.骑车的同学从出发到追上步行的同学用了20分钟

    D.步行同学的速度是6千米/小时，骑车同学的速度是千米/小时.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】凸四边形的四个顶点满足：每一个顶点到其他三个顶点距离之积都相等．则四边形一定是（ ）

    A. 正方形 B. 菱形 C. 等腰梯形 D. 矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEF中，满足AB=DE，∠B=∠E，如果要判定这两个三角形全等，那么添加的条件不正确的是（ ）

    A. ∠A=∠D B. ∠C=∠F C. BC=EF D. AC=DF

    查看答案和解析>>

    同步练习册答案