
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.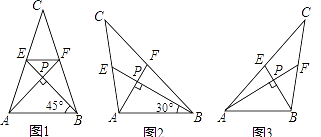
(1)【特例探索】
如图1,当∠ABE=45°,c=2 ![]() 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)【拓展应用】
如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
【答案】
(1)2 ![]() ;2
;2 ![]() ;2
;2 ![]() ;2
;2 ![]()
(2)
猜想:a 2,b2,c2三者之间的关系是:a2+b2=5c2,
证明:如图3,连接EF,
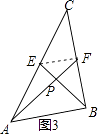
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EF= ![]() AB=
AB= ![]() c.
c.
∴ ![]()
设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2①
在Rt△APE中,(2m)2+n2=( ![]() )2②
)2②
在Rt△BPF中,m2+(2n)2=( ![]() )2③
)2③
由①得:m2+n2= ![]() ,由②+③得:5( m2+n2)=
,由②+③得:5( m2+n2)= ![]() ,
,
∴a 2+b2=5 c2;
(3)
如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,
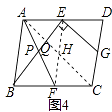
∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=2 ![]() ,
,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE= ![]() AD,BF=
AD,BF= ![]() BC,
BC,
∴AE=BF=CF= ![]() AD=
AD= ![]() ,
,
∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
在△AEH和△CFH中, 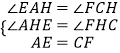 ,
,
∴△AEH≌△CFH,
∴EH=FH,
∴EP,AH分别是△AFE的中线,
由(2)的结论得:AF2+EF2=5AE2,
∴AF2=5( ![]() )2﹣EF2=16,
)2﹣EF2=16,
∴AF=4.
【解析】解:(1.)∵AF⊥BE,∠ABE=45°,
∴AP=BP= ![]() AB=2,
AB=2,
∵AF,BE是△ABC的中线,
∴EF∥AB,EF= ![]() AB=
AB= ![]() ,
,
∴∠PFE=∠PEF=45°,
∴PE=PF=1,
在Rt△FPB和Rt△PEA中,
AE=BF= ![]() =
= ![]() ,
,
∴AC=BC=2 ![]() ,
,
∴a=b=2 ![]() ,
,
如图2,连接EF,
同理可得:EF= ![]() ×4=2,
×4=2,
∵EF∥AB,
∴△PEF~△ABP,
∴ ![]() ,
,
在Rt△ABP中,
AB=4,∠ABP=30°,
∴AP=2,PB=2 ![]() ,
,
∴PF=1,PE= ![]() ,
,
在Rt△APE和Rt△BPF中,
AE= ![]() ,BF=
,BF= ![]() ,
,
∴a=2 ![]() ,b=2
,b=2 ![]() ,
,
所以答案是:2 ![]() ,2
,2 ![]() ,2
,2 ![]() ,2
,2 ![]() ;
;
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
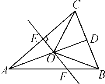
A. 3对 B. 4对 C. 5对 D. 6对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 ![]() 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 ![]() 的值为 .
的值为 . 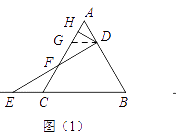
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值.
的值.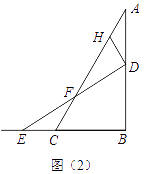
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 ![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).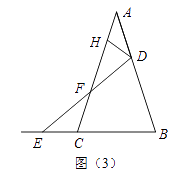
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) 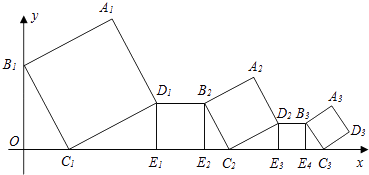
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 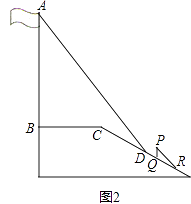
查看答案和解析>>
科目:初中数学 来源: 题型:
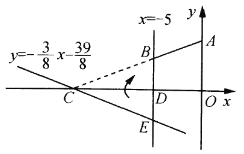
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() .点
.点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的表达式;
的表达式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,
的位置,![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班长调查了三班近 10 天的数学课堂小测验,在这 10 天,小测验的不及格人数为(单位:个)0,2,0, 3,1,1,0,2,5,1.在这 10 天中小测验不及格的人数( )
A. 中位数为 1.5 B. 方差为 1.5 C. 极差为 1.5 D. 标准差为 1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() =90°,
=90°,![]() 于
于![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() ;上述结论中正确的个数是( )
;上述结论中正确的个数是( )
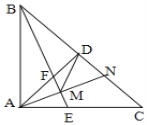
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com