
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=![]() ,求sin 2α的值.
,求sin 2α的值.
小娟是这样给小芸讲解的:
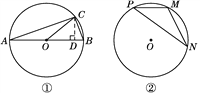
如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=![]() =
=![]() .易得∠BOC=2α.设BC=x,则AB=3x,AC=2
.易得∠BOC=2α.设BC=x,则AB=3x,AC=2![]() x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=
x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=![]() =________.
=________.
【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=![]() ,求sin 2β的值.
,求sin 2β的值.
【答案】![]() ;
;![]() ;sin 2β=
;sin 2β=![]() .
.
【解析】试题分析:(1)如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() =
=![]() ,可设BC=x,则AB=3x.利用面积法求出CD=
,可设BC=x,则AB=3x.利用面积法求出CD=![]() ,在Rt△COD中, sin2α=
,在Rt△COD中, sin2α=![]() =
= .(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.先证明∠MON=2∠Q=2β,在Rt△QMN中,由sinβ=
.(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.先证明∠MON=2∠Q=2β,在Rt△QMN中,由sinβ=![]() ,设MN=3k,则NQ=5k,易得OM=
,设MN=3k,则NQ=5k,易得OM=![]() NQ=
NQ=![]() ,可得MQ=
,可得MQ=![]() =4k,由
=4k,由![]() MNMQ=
MNMQ=![]() NQMR,求出MR=
NQMR,求出MR=![]() ,在Rt△MRO中,根据sin2β=sin∠MON=
,在Rt△MRO中,根据sin2β=sin∠MON=![]() ,计算即可求得sin 2β的值.
,计算即可求得sin 2β的值.
试题解析:
(1)![]() ;
;![]()
(2)如图,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.
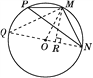
在⊙O中,∠NMQ=90°.
∵∠Q=∠P=β,
∴∠MON=2∠Q=2β.
在Rt△QMN中,
∵sin β=![]() ,
,
∴设MN=3k,则NQ=5k,
∴MQ=![]() =4k,
=4k,
OM=![]() NQ=
NQ=![]() k.
k.
∵S△NMQ=![]() MN·MQ=
MN·MQ=![]() NQ·MR,
NQ·MR,
∴3k·4k=5k·MR.
∴MR=![]() k.
k.
在Rt△MRO中,
sin 2β=sin ∠MON=![]() =
=![]() =
=![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:
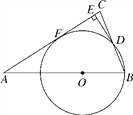
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
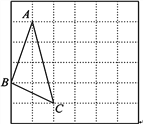
【题目】在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-1,-1),(1,-2),将△ABC绕着点C顺时针旋转90°得到△A′B′C′.
(1)在图中画出△A′B′C′并写出点A的对应点A′坐标;
(2)求出在△ABC旋转的过程中,点A经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下面直角坐标系中,已知![]()

(1)求![]() 的面积
的面积
(2)若以点![]() 为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点
为顶点画平行四边形,则请你“利用平移的知识”直接写出符合条件的所有的平行四边形的第四个顶点![]() 的坐标
的坐标
(3)是否存在![]() 轴上的点
轴上的点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,若存在,求出点
倍,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
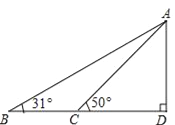
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?答:我抽取的2张卡片是________、________,乘积的最大值为________.
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?答:我抽取的2张卡片是________、________,商的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果是3n+5;②n为偶数时,结果是![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如取n=26,则有如图的结果,那么当n=2015,求第2015次“F”运算的结果是 .
为奇数的正整数),并且运算重复进行.例如取n=26,则有如图的结果,那么当n=2015,求第2015次“F”运算的结果是 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com