

分析 (1)根据统计图中的数据可以求得本次比赛获奖的人数,也可得到获得四等奖的人数,从而可将条形图补充完整;
(2)根据条形图可以得到在扇形统计图中,二等奖对应的圆心角的度数;
(3)根据题意可以求得求这两名同学均获得一等奖的概率.
解答 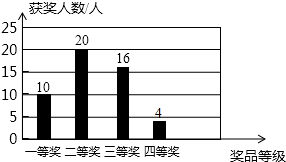 解:(1)10÷20%=50,
解:(1)10÷20%=50,
故答案为:50,
四等奖的学生有:50-10-20-16=4,
补全的条形图如右图所示,
(2)在扇形统计图中,二等奖对应的圆心角的度数是:360°×$\frac{20}{50}$=144°,
故答案为:144°;
(3)在上述获奖同学中任意抽取两名,第一位同学是一等奖的概率是$\frac{10}{50}$,第二位同学是一等奖的概率是:$\frac{9}{49}$,
故这两名同学均获得一等奖的概率是:$\frac{10}{50}×\frac{9}{49}=\frac{9}{245}$,
即这两名同学均获得一等奖的概率是$\frac{9}{245}$.
点评 本题考查列表法与树状图法、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,设A为反比例函数$y=\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为y=-$\frac{3}{x}$.
如图所示,设A为反比例函数$y=\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则这个反比例函数解析式为y=-$\frac{3}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,菱形ABCD 中,过AD 的中点 E作AC 的垂线EF,交AB 于点 M,交CB 的延长线于点F.如果FB的长是 $\sqrt{2}$,∠AEM=30°.求菱形ABCD 的周长和面积.
已知:如图,菱形ABCD 中,过AD 的中点 E作AC 的垂线EF,交AB 于点 M,交CB 的延长线于点F.如果FB的长是 $\sqrt{2}$,∠AEM=30°.求菱形ABCD 的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥3 | B. | x≤2 | C. | x≥2 | D. | 2≤x≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com