
【题目】如图1,已知在平面直角坐标系中,A(![]() ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=![]() .
.

(1)求直线AD的解析式和线段BD所在直线的解析式.
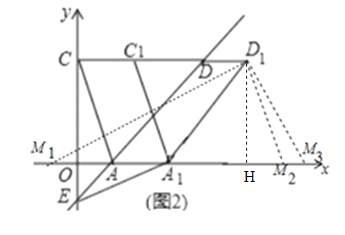
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
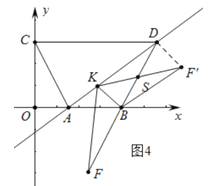
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的![]() .
.
【答案】(1)y=![]() x﹣
x﹣![]() .y=2x﹣8(2)M1(﹣
.y=2x﹣8(2)M1(﹣![]() ,0),M2(
,0),M2(![]() ,0),M3(
,0),M3(![]() ,0)(3)
,0)(3)![]() 或
或![]()
【解析】
(1)如图1中,作DH⊥x轴于H.解直角三角形求出AH,即可求出点D坐标,只可以待定系数法即可解决问题;
(2)求出直线EA1的解析式可得A1坐标,分两种情形当A1D1=AM=5时,当D1A1=D1M时,分别求解即可解决问题;
(3)分两种情形,①若翻折后,点F′在直线AD上方,记F′B与DK交于点S,连接F'D,只要证明四边形DBKF′是平行四边形,可得KF=KF′=DB=![]() ,设K(m,
,设K(m,![]() m﹣
m﹣![]() ),F(
),F(![]() ,﹣3),可得(m﹣
,﹣3),可得(m﹣![]() )2+(
)2+(![]() m﹣
m﹣![]() +3)2=(
+3)2=(![]() )2,解方程即可;
)2,解方程即可;
②若翻折后,点F′在直线DA下方,记F′K与BD交于点S,连接DF′,如图4,四边形BKDF′是平行四边形,可得DK=BF′=BF=BD=![]() .
.
(1)如图1中,作DH⊥x轴于H.

∵CD∥OH,OC∥DH,∴四边形CDHO是平行四边形.
∵∠DHO=90°,∴四边形CDHO是矩形,∴DH=OC=3,CD=OH.在Rt△ADH中,tan∠DAH=![]() =
=![]() ,∴AH=4,OH=OA+AH=
,∴AH=4,OH=OA+AH=![]() ,∴D(
,∴D(![]() ,3),设直线AD的解析式为y=kx+b,则有
,3),设直线AD的解析式为y=kx+b,则有 ,解得:
,解得: ,∴直线AD的解析式为y=
,∴直线AD的解析式为y=![]() x﹣
x﹣![]() .
.
设直线BD的解析式为y=k′x+b′,则有 ,解得:
,解得:![]() ,∴直线BD的解析式为y=2x﹣8.
,∴直线BD的解析式为y=2x﹣8.
(2)如图2中,∵直线AD的解析式为y=![]() x﹣
x﹣![]() .
.
∵C(0,3),A(![]() ,0),∴直线AC是解析式为y=﹣2x+3.
,0),∴直线AC是解析式为y=﹣2x+3.
∵AC∥A1C1,A1C1⊥EA1,∴AC⊥EA1,∴直线EA1的解析式为y=![]() x﹣
x﹣![]() ,∴A1(
,∴A1(![]() ,0).
,0).
分两种情况讨论:
①当A1D1=AM=5时,以A1为圆心,A1D1为半径作圆,交x轴于M1,M2,则M1(﹣![]() ,0),M2(
,0),M2(![]() ,0);
,0);
②当D1A1=D1M时,过D1作D1H⊥x轴于H,AD=![]() =5,∴A1D1=AD=5.
=5,∴A1D1=AD=5.
∵ HD1=3,∴A1H=4,∴A1M=2 A1H =8,∴OM=OA1+A1M=![]() =
=![]() ,∴M3(
,∴M3(![]() ,0).
,0).
综上所述:满足条件的点M的坐标M1(﹣![]() ,0),M2(
,0),M2(![]() ,0),M3(
,0),M3(![]() ,0).
,0).
(3)如图3中,①若翻折后,点F′在直线AD上方,记F′B与DK交于点S,连接F'D,S△KSB=![]() S△DFK=
S△DFK=![]() S△DBK=
S△DBK=![]() S△BKF′′,即S△DBK=S△F′BK=S△BKF,∴SB=SF′,KS=DS,∴四边形DBKF′是平行四边形,∴KF=KF′=DB=
S△BKF′′,即S△DBK=S△F′BK=S△BKF,∴SB=SF′,KS=DS,∴四边形DBKF′是平行四边形,∴KF=KF′=DB=![]() ,设K(m,
,设K(m,![]() m﹣
m﹣![]() ).
).
∵F(![]() ,﹣3),∴(m﹣
,﹣3),∴(m﹣![]() )2+(
)2+(![]() m﹣
m﹣![]() +3)2=(
+3)2=(![]() )2,解得:m=
)2,解得:m=![]() 或﹣
或﹣![]() ,∴K(
,∴K(![]() ),∴DK=
),∴DK=![]() =
=![]()

②若翻折后,点F′在直线DA下方,记F′K与BD交于点S,连接DF′,如图4.
∵S△KBS=![]() S△DGK=
S△DGK=![]() S△DBK=
S△DBK=![]() S△KBF′,即S△BKS=S△BSF′=S△DSK,∴KS=SF′,SB=SD,∴四边形BKDF′是平行四边形,∴DK=BF′=BF=BD=
S△KBF′,即S△BKS=S△BSF′=S△DSK,∴KS=SF′,SB=SD,∴四边形BKDF′是平行四边形,∴DK=BF′=BF=BD=![]() .
.
综上所述:满足条件的DK的值为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如下表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
一般地,![]() 该种作物种子中大约有多少是不能发芽的?
该种作物种子中大约有多少是不能发芽的?
查看答案和解析>>
科目:初中数学 来源: 题型:
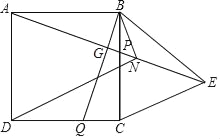
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
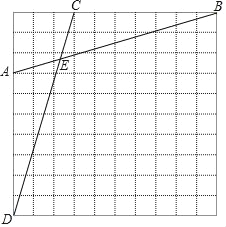
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C,D均在格点上,AB与CD相交于点E.
(Ⅰ)AB的长等于 ;
(Ⅱ)点F是线段DE的中点,在线段BF上有一点P,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)当![]() 时,求该抛物线与坐标轴的交点的坐标;
时,求该抛物线与坐标轴的交点的坐标;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若直线![]() 与二次函数的图象交于
与二次函数的图象交于![]() 、
、![]() 两点,问线段
两点,问线段![]() 的长度是否是定值?如果是,求出其长度;如果不是,请说明理由.
的长度是否是定值?如果是,求出其长度;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com