
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
分析 (1)根据中位数的定义,先将数据重新排列,再找到最中间位置的数即可得;
(2)根据方差的定义即可得;
(3)可从优秀率、中位数、方差等方面分析、评定,即可得.
解答 解:(1)甲班成绩从小到大排列为:89、96、97、100、118,
∴甲班5名学生比赛成绩的中位数是97,
乙班成绩从小到大排列为:91、95、100、104、110,
∴乙班5名学生比赛成绩的中位数是100;
(2)∵$\overline{{x}_{甲}}$=$\frac{500}{5}$=100,
∴${{S}_{甲}}^{2}$=$\frac{1}{5}$[(89-100)2+(100-100)2+(96-100)2+(118-100)2+(97-100)2]=94,
∵$\overline{{x}_{乙}}$=$\frac{500}{5}$=100,
∴${S}_{{乙}^{2}}$=$\frac{1}{5}$[(100-100)2+(95-100)2+(110-100)2+(91-100)2+(104-100)2]=44.4
∴${{S}_{甲}}^{2}$>${S}_{{乙}^{2}}$,
∴乙班比赛数据的方差小;
(3)冠军奖应发给乙班,
∵乙班5名学生的比赛成绩的优秀率比甲班高,中位数比甲班大,方差比甲班小,
∴综合以上各种情况,乙班踢毽子的水平较高.
点评 本题主要考查中位数、平均数、方差,熟练掌握中位数和方差的定义并熟记方差的计算公式是解题的关键.


科目:初中数学 来源: 题型:解答题
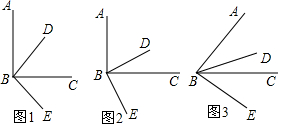
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
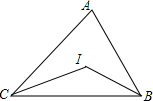 如图,在△ABC中,∠ABC、∠ACB的平分线相交于点I,根据下列条件,求∠BIC的度数.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于点I,根据下列条件,求∠BIC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
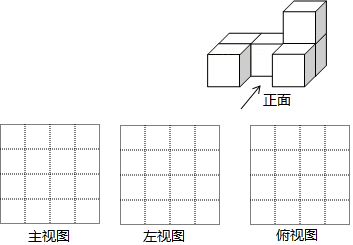
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
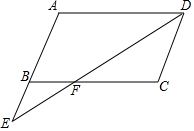 如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.
如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
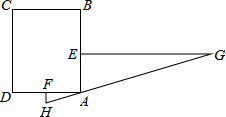 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com