
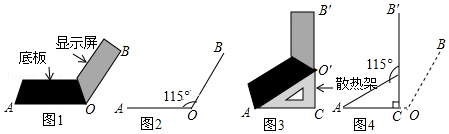
分析 (1)如图3中,在Rt△AO′C中,解直角三角形即可;
(2)如图2,过B作BD⊥AO交AO的延长线于D,在Rt△OBD中,解直角三角形即可;
(3)如图4,过O′作EF∥OB交AC于E,易知∠FEA=∠BOA=115°,推出∠FOB′=∠EO′C=∠FEA-∠O′CA=115°-90°=25°;
解答 解:(1)如图3中,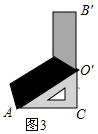
∵B′O′⊥AC,垂足为C,∠AO′B=115°,
∴∠AO′C=65°,
∵cos∠CO′A=$\frac{O′C}{O′A}$,
∴O′C=O′A•cos∠CO′A=20•cos65°=8.46≈8.5(cm);
(2)如图2,过B作BD⊥AO交AO的延长线于D,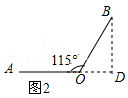
∵∠AOB=115°,
∴∠BOD=65°,
∵sin∠BOD=$\frac{BD}{OB}$,
∴BD=OB•sin∠BOD=20×sin65°=18.12,
∴O′B′+O′C-BD=20+8.46-18.12=10.34≈10.3(cm),
∴显示屏的顶部B′比原来升高了10.3cm;
(3)如图4,过O′作EF∥OB交AC于E,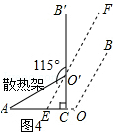
∴∠FEA=∠BOA=115°,
∴∠FOB′=∠EO′C=∠FEA-∠O′CA=115°-90°=25°,
∴显示屏O′B′应绕点O′按顺时针方向旋转25度.
点评 本题考查解直角三角形的应用、解题的关键是灵活运用所学知识解决问题,学会添加辅助线,构造直角三角形解决问题,属于中考常考题型.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{30}{x}$-$\frac{30}{(1+20%)x}$=5 | B. | $\frac{30}{x}$-$\frac{30}{20%x}$=5 | C. | $\frac{30}{20%x}$+5=$\frac{30}{x}$ | D. | $\frac{30}{(1+20%)x}$-$\frac{30}{x}$=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y=4}\\{xy=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=2}\\{x+y=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-2y=4}\\{x=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-\frac{3}{3}y=2}\\{2y=x}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com