
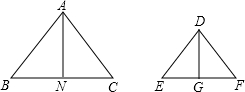
 已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF.
已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF. 分析 根据$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$与勾股定理证明△ABN∽△DEG,由此可得∠BAN=∠EDG;同理可证∠CAN=∠FDG,则:∠BAC=∠EDF,再由“两边对应成比例且夹角相等的两个三角形相似”证明结论.
解答 证明:∵$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,设$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$=k
∴AB=kDE,AC=kDF,AN=kDG,
在Rt△ABN 与Rt△DEG中,
BN2=AB2-AN2,EG2=DE2-DG2
∴BN2=k2DE2-k2DG2=k2(DE2-DG2)
∴$\frac{B{N}^{2}}{E{G}^{2}}$=k2,
∴$\frac{BN}{EG}=k$
∴在△ABN与△DEG中,$\left\{\begin{array}{l}{∠ANB=∠DGE=90°}\\{\frac{AN}{DG}=\frac{BN}{EG}}\end{array}\right.$
∴△ABN∽△DEG
∴∠BAN=∠EDG.
同理可证∠CAN=∠FDG.
∴∠BAC=∠EDF,且$\frac{AB}{DE}$=$\frac{AC}{DF}$
∴△ABC∽△DEF
点评 本题考查了相似三角形的判定与性质,解题的关键是掌握相似三角形的判定方法与性质.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与x轴的负半轴相交于点A(-1,0),与y轴相交于点B(0,3).
如图,抛物线y=-x2+bx+c与x轴的负半轴相交于点A(-1,0),与y轴相交于点B(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com