
【题目】如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
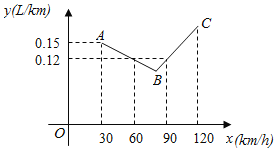
(1)当30≤x≤120时,求y与x之间的函数表达式;
(2)该汽车的速度是多少时,耗油量最低?最低是多少.
【答案】(1)y=0.002x﹣0.06;(2)速度是80km/h时,该汽车的耗油量最低,最低是0.1L/km.
【解析】
(1)分别设出AB段和BC段的一次函数解析式,利用待定系数法即可解决问题;
(2)观察图形发现,两线段的交点即为最低点,因此求两函数解析式组成的方程组的解即可.
(1)设AB的解析式为:y=kx+b,
把(30,0.15)和(60,0.12)代入y=kx+b中得:
![]() ,解得
,解得![]() ,
,
∴AB段一次函数的解析式为:y=﹣0.001x+0.18,
设BC的解析式为:y=mx+n,
把(90,0.12)和(100,0.14)代入y=mx+n中得:
![]() ,解得
,解得![]() ,
,
∴BC段一次函数的解析式为:y=0.002x﹣0.06;
(2)根据题意得
![]() ,解得
,解得![]() ,
,
答:速度是80km/h时,该汽车的耗油量最低,最低是0.1L/km.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】根据图中给出的数轴解答问题:
![]()
(1)请你根据图中A,B两点的位置,分别写出他们所表示的有理数为 ;
(2)观察数轴,与点A的距离为4的点表示的数是 ;
(3)如果将数轴折叠,使得点A与表示﹣2的点重合,则点B与表示数 的点重合;
(4)如果数轴上M,N两点之间的距离为2020(M在N的左侧),且M,N两点经过(3)中折叠后互相重合,则M,N两点所表示的数分别是 , .![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣81)+(﹣29)
(2)﹣7+13﹣6+20
(3)1+(﹣![]() )﹣(﹣
)﹣(﹣![]() )﹣
)﹣![]()
![]()
(4)﹣0.5﹣(﹣3)+2.75﹣(+7)
(5)(+16)+(﹣3)﹣|﹣8|+|﹣12|﹣(﹣5)
(6)(﹣0.25)×(﹣2)×(﹣![]() )×(+0.8)
)×(+0.8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面给出的数轴,解答下面的问题:
![]()
⑴ 请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: B: ;
⑵ 观察数轴,与点A的距离为4的点表示的数是: ;
⑶ 若将数轴折叠,使得A点与-3表示的点重合,则B点与数 表示的点重合;
⑷ 若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E为CD上一点,连接BE,AD∥BE,连接BD,BD平分∠ABE,BF平分∠ABC交CD于点F, ∠ABC=100°,∠DBF=14°,∠ADC的度数为_______°.
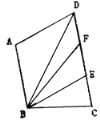
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
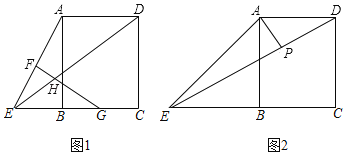
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别为边AD,BC上的点,AE=CF,对角线AC平分∠ECF.
(1)求证:四边形AECF为菱形.
(2)已知AB=4,BC=8,求菱形AECF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com