Question

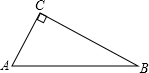
根据下列条件解直角三角形．在Rt△ABC中，∠C=90°
（1）c=20，∠A=45°     
（2）a=36，∠B=30°

Answer 1

解：（1）∵∠C=90°，∠A=45°，
∴∠B=45°，
∴a=b，
∵c²=a²+b²，c=20，
∴a=b=10；

（2）∵∠C=90°，∠B=30°，
∴∠A=60°，
∴c=a÷sinA=36÷=24，
∴b=c=12．
分析：（1）根据直角三角形两锐角互余求出∠B，然后求出a=b，再利用勾股定理列式计算即可得解；
（2）直角三角形两锐角互余求出∠A，然后根据∠A的正弦求出c，再根据直角三角形30°角所对的直角边等于斜边的一半可得b=c．
点评：本题考查了解直角三角形，主要利用了锐角三角函数和勾股定理．