
【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
【答案】(1)8;(2)|x-3|(或填|3-x|);(3)6;![]() ;(4)x<4或x>2.
;(4)x<4或x>2.
【解析】
(1)根据两点间的距离公式即可求解;
(2)根据两点间的距离公式可求A与B两点的距离;
(3)|x+4|即x与4的差的绝对值,它可以表示数轴上x与4之间的距离.|x2|即x与2的差的绝对值,它也可以表示数轴上x与2之间的距离.借助数轴,我们可以得到正确答案;
(4)借助数轴,我们可以得到正确答案:x<4或x>2.
解:(1)A与B两点间的距离是|6(2)|=8.
故答案为:8;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点的距离可以表示为|x3|或|3-x|,
故答案为:|x3|或|3-x|;
(3)如图:|x+4|表示数轴上表示x的点与4之间的距离,|x2|表示数轴上表示x的点与2之间的距离,若|x+4|+|x2|的值最小,x应在数轴上4与2之间,因此最小值为6,
答:|x+4|+|x2|的最小值为6,取得最小值时x的取值范围为4≤x≤2;
故答案为6,4≤x≤2;

(4)借助数轴分析,可以得到满足|x+4|+|x2|>6的x的取值范围为:x<4或x>2,
故答案为:x<4或x>2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣x+4与x轴交于点A,B,B点的坐标为(﹣4,0),与y轴交于点C.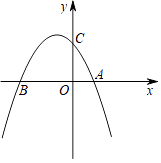
(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级学生课外活动情况,随机调查了该校若干名学生,调查他们喜欢各类课外活动的情况(课外活动分为四类:A﹣﹣喜欢打乒乓球的人,B﹣﹣喜欢踢足球的人,C﹣﹣喜欢打篮球的人,D﹣﹣喜欢其他的人),并将调查结果绘制成如下两幅不完整的统计图.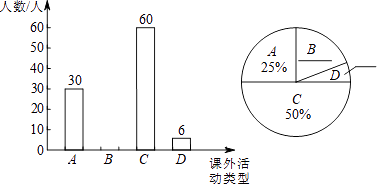
根据统计图信息完成下列问题:
(1)调查的学生人数为人.
(2)补全条形统计图和扇形统计图.
(3)若该校七年级共有600人,请估计七年级学生中喜欢打乒乓球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 、
、![]() 、
、![]() 都是射线,
都是射线,![]() ,
,![]() 与
与![]() 互为余角.
互为余角.

(1)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(2)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(3)![]() 与
与![]() 有何关系?请证明你的结论.
有何关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的正方形ABCD的对角线BD上作一点P,使PA+PC最小;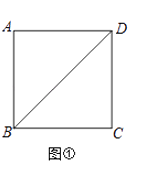
(2)如图②,点P为矩形ABCD的对角线BD上一动点,AB=2,BC=2 ![]() ,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.
,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.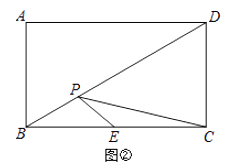
(3)如图③,李师傅有一块边长为1000米的菱形ABCD采摘园,AC=1200米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出的点P位置,并求出这个最短距离;若不存在,请说明理由.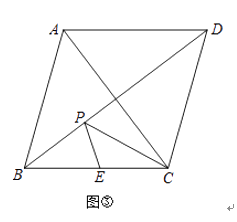
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
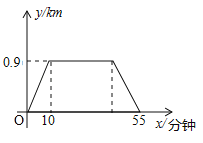
【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com