
 ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻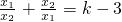 �����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�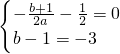 ��
�� ��
�� ��
��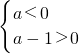 ��
�� ��
�� ��
�� +
+ =3+
=3+ =
= ��a��0��a��-
��a��0��a��- ����a������
����a������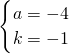 ��
��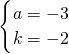 ��
�� =
= �����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻
�����ɵó�a��b��ֵ�������ó�ͼ���ϵIJ����㣻


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�콭��ʡ�������о��꼶�������ʼ���ѧ�Ծ����������� ���ͣ������
�¶��壺��x0=ax02+bx0+c��������Ƶ�(x0,x0)Ϊ������y=ax2+bx+c (a��0)�ϵIJ�����.��������C�Ľ���ʽΪ��y=ax2+(b+1)x+(b -1)(a��0).
��1��������C����(0��-3)�������������C����ƽ�� ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
��2����������ʵ��b��ʵ��aӦ��ʲô��Χ�ڣ�����ʹ������C������������ͬ�IJ����㣿
��3����aΪ������������a+b+1=0����������C��x��������ĺ�����ֱ�Ϊx1, x2���Ƿ��������k��ʹ�� �����������ڣ����k��ֵ���������ڣ���˵������.
�����������ڣ����k��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�꽭��ʡ�������о��꼶�������ʼ���ѧ�Ծ��������棩 ���ͣ������
�¶��壺��x0=ax02+bx0+c��������Ƶ�(x0,x0)Ϊ������y=ax2+bx+c (a��0)�ϵIJ�����.��������C�Ľ���ʽΪ��y=ax2+(b+1)x+(b -1)(a��0).
��1��������C����(0��-3)�������������C����ƽ�� ����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
����λ���䶥��ǡ����y���ϣ���������C�Ľ���ʽ�����ϵIJ����㣻
��2����������ʵ��b��ʵ��aӦ��ʲô��Χ�ڣ�����ʹ������C������������ͬ�IJ����㣿
��3����aΪ������������a+b+1=0����������C��x��������ĺ�����ֱ�Ϊx1, x2���Ƿ��������k��ʹ�� �����������ڣ����k��ֵ���������ڣ���˵������.
�����������ڣ����k��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com