
阅读:如图所示,△ABC内接于⊙O,∠CAE=∠B.

求证:AE与⊙O相切于点A.
证明:作直径AF,连结FC,则∠ACF= .
.
∴∠AFC+∠CAF=
∵∠B=∠AFC
∴∠B+∠CAF=
又∵∠CAE=∠B
∴∠CAE+∠CAF= .
.
即AE与⊙O相切于点A.
问题:通过阅读得到的启示证明下题(阅读中的结论可直接应用).
如图所示,已知△ABC内接于⊙O,P是CB延长线上一点,连结AP,且PA2=PB·PC.求证:PA是⊙O的切线.

科目:初中数学 来源: 题型:阅读理解
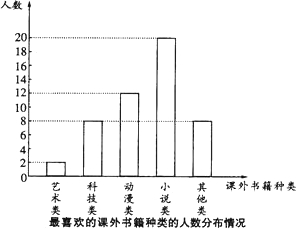 抽取部分同学进行问卷调查,并将调查问卷适当整理后绘制成如图所示的条形统计图.
抽取部分同学进行问卷调查,并将调查问卷适当整理后绘制成如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 20、阅读材料,解答问题.
20、阅读材料,解答问题.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练八年级数学下册(北师大版) 题型:044
(1)阅读:如图所示△ABC中,∠BAC=![]() ,AB=AC,作∠ABC的平分线交AC于点D,这个点D是线段AC的黄金分割点,且AD>CD.
,AB=AC,作∠ABC的平分线交AC于点D,这个点D是线段AC的黄金分割点,且AD>CD.
(2)在(1)的图形中,还有哪些线段相等,△BCD的三内角各是多少度?
(3)在(1)中,求BC∶AC和BC∶CD的值;
(4)利用(1)的结论,你能作出(1)中线段BD的黄金分割点吗?请作出来,并保留作图痕迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com