
已知,如图双曲线 (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线 (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是__________;
(2)四边形ABDC的面积为__________.
(1)AB∥CD;(2)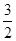 .
.
解析试题分析:(1)首先过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,由双曲线y=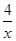 (x>0)与直线EF交于点A、点B,且AE=AB=BF,可设点A的坐标为(m,
(x>0)与直线EF交于点A、点B,且AE=AB=BF,可设点A的坐标为(m, ),得到点B的坐标为:(2m,
),得到点B的坐标为:(2m, 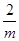 ),则可由S△OAB=S△OAM+S梯形AMNB﹣S△OBN,求得△AOB的面积=3,根据DH∥BN易得△ODH∽△OBN,可得(
),则可由S△OAB=S△OAM+S梯形AMNB﹣S△OBN,求得△AOB的面积=3,根据DH∥BN易得△ODH∽△OBN,可得( )2=
)2=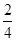 =
= ,继而可得
,继而可得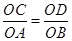 ,所以AB∥CD;
,所以AB∥CD;
(2)由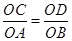 ,∠COD=∠AOB则可证得△COD∽△AOB,然后由相似三角形面积比等于相似比的平方,求得S四边形ABDC=
,∠COD=∠AOB则可证得△COD∽△AOB,然后由相似三角形面积比等于相似比的平方,求得S四边形ABDC=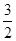 .
.
故答案是(1)AB∥CD;(2)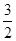 .
.
考点:反比例函数与一次函数的交点问题.


科目:初中数学 来源: 题型:填空题
如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com