
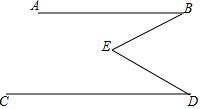
 如图,已知∠BED=∠B+∠D,试说明AB∥CD.
如图,已知∠BED=∠B+∠D,试说明AB∥CD. 分析 被判断平行的两直线缺少由“三线八角”而产生的被截直线,所以先延长BE交CD于F,根据三角形外角的性质可得∠BED=∠D+∠EFD.已知∠BED=∠B+∠D,所以∠B=∠EFD.再根据内错角相等两直线平行即可证得AB∥CD.
解答 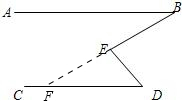 证明:如图,延长BE交CD于F.
证明:如图,延长BE交CD于F.
∵∠BED是△DEF的外角,
∴∠BED=∠D+∠EFD(三角形的一个外角等于和它不相邻的两个内角和),
又∠BED=∠B+∠D,
∴∠B=∠EFD(等量代换),
∴AB∥CD(内错角相等,两直线平行).
点评 本题主要考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.


科目:初中数学 来源: 题型:解答题
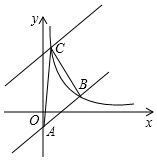 如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)
如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.
小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三个内角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三条中线的交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com