
【题目】等腰![]() 中,
中,![]() ,作
,作![]() 的外接圆⊙O.
的外接圆⊙O.
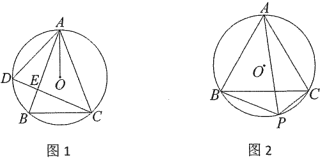
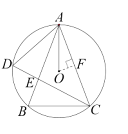
(1)如图1,点![]() 为
为![]() 上一点(不与A、B重合),连接AD、CD、AO,记
上一点(不与A、B重合),连接AD、CD、AO,记![]() 与
与![]() 的交点为
的交点为![]() .
.
①设![]() ,若
,若![]() ,请用含
,请用含![]() 与
与![]() 的式子表示
的式子表示![]() ;
;
②当![]() 时,若
时,若![]() ,求
,求![]() 的长;
的长;
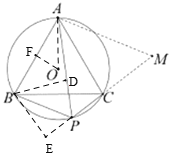
(2)如图2,点![]() 为
为![]() 上一点(不与B、C重合),当BC=AB,AP=8时,设
上一点(不与B、C重合),当BC=AB,AP=8时,设![]() ,求
,求![]() 为何值时,
为何值时,![]() 有最大值?并请直接写出此时⊙O的半径.
有最大值?并请直接写出此时⊙O的半径.
【答案】(1)①![]() ;②
;②![]() ;(2)PB=5时,S有最大值,此时⊙O的半径是
;(2)PB=5时,S有最大值,此时⊙O的半径是![]() .
.
【解析】
(1)①连接BO、CO,利用SSS可证明△ABO≌△ACO,可得∠BAO=∠CAO=y,利用等腰三角形的性质及三角形内角和定理可用y表示出∠ABC,由圆周角定理可得∠DCB=∠DAB=x,根据![]() 即可得答案;
即可得答案;
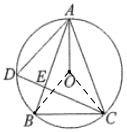
②过点![]() 作
作![]() 于点
于点![]() ,根据垂径定理可得AF的长,利用勾股定理可求出OF的长,由(1)可得
,根据垂径定理可得AF的长,利用勾股定理可求出OF的长,由(1)可得![]() ,由AB⊥CD可得n=90°,即可证明y=x,根据AB⊥CD,OF⊥AC可证明△AED∽△AFO,设DE=a,根据相似三角形的性质可
,由AB⊥CD可得n=90°,即可证明y=x,根据AB⊥CD,OF⊥AC可证明△AED∽△AFO,设DE=a,根据相似三角形的性质可![]() ,由∠D=∠B,∠AED=∠CEB=90°可证明△AED∽△CEB,设
,由∠D=∠B,∠AED=∠CEB=90°可证明△AED∽△CEB,设![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,根据线段的和差关系和勾股定理列方程组可求出a、b的值,根据△AED∽△AFO即可求出AD的值;
,根据线段的和差关系和勾股定理列方程组可求出a、b的值,根据△AED∽△AFO即可求出AD的值;
(2)延长![]() 到
到![]() ,使得
,使得![]() ,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,根据BC=AB可得三角形ABC是等边三角形,根据圆周角定理可得∠APM=60°,即可证明△APM是等边三角形,利用角的和差关系可得∠BAP=∠CAM,利用SAS可证明△BAP≌△CPM,可得BP=CM,即可得出PB+PC=AP,设
,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,根据BC=AB可得三角形ABC是等边三角形,根据圆周角定理可得∠APM=60°,即可证明△APM是等边三角形,利用角的和差关系可得∠BAP=∠CAM,利用SAS可证明△BAP≌△CPM,可得BP=CM,即可得出PB+PC=AP,设![]() ,则
,则![]() ,利用∠APB和∠BPE的正弦可用x表示出BD、BE的长,根据
,利用∠APB和∠BPE的正弦可用x表示出BD、BE的长,根据![]() 可得S与x的关系式,根据二次函数的性质即可求出S取最大值时x的值,利用∠BPA的余弦及勾股定理可求出AB的长,根据等边三角形的性质及垂径定理求出OA的长即可得答案.
可得S与x的关系式,根据二次函数的性质即可求出S取最大值时x的值,利用∠BPA的余弦及勾股定理可求出AB的长,根据等边三角形的性质及垂径定理求出OA的长即可得答案.
(1)①连接BO,CO,
∵![]() ,且
,且![]() 为公共边,
为公共边,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∵![]() ,
,
∴![]()
∴![]() .
.
②过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴△AED∽△AFO,
∴![]() =,即
=,即![]() ,
,
设![]() ,则
,则![]()
∵![]() ,
,
∴△AED∽△CEB,
∴![]() ,即
,即![]()
设![]() ,则
,则![]() ,
,
∴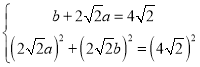
解得:![]() 或
或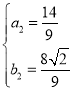 ,
,
∵a>0,b>0,
∴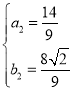 ,即DE=
,即DE=![]() ,
,
∵△AED∽△AFO,
∴![]() ,
,
∴AD=![]() =3
=3![]() =
=![]() .
.
(2)延长![]() 到
到![]() ,使得
,使得![]() ,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,
,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,
∵BC=AB,AB=AC,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵∠BAP+∠PAC=∠CAM+∠PAC=60°,
∴![]()
在△BAP和△CAM中,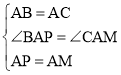 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,则
,则![]() ,
,
∵∠APB=∠ACB=60°,∠APM=60°,
∴∠BPE=60°,
∴BE=PB·sin60°=![]() ,PD=PB·sin60°=
,PD=PB·sin60°=![]() ,
,
∵![]() ,
,
∴S=![]() PC·BE+
PC·BE+![]() ×
×![]() AP·BD=
AP·BD=![]() ,
,
∴当![]() 时,即PB=5时,S有最大值,
时,即PB=5时,S有最大值,
∴BD=![]() =
=![]() ,PD=PB·cos60°=
,PD=PB·cos60°=![]() ,
,
∴AD=AP-PD=![]() ,
,
∴AB=![]() =7,
=7,
∵△ABC是等边三角形,O为△ABC的外接圆圆心,
∴∠OAF=30°,AF=![]() AB=
AB=![]() ,
,
∴OA=![]() =
=![]() .
.
∴此时![]() 的半径是
的半径是![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
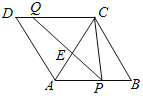
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
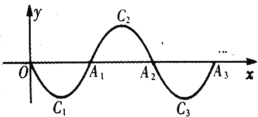
【题目】如图,二次函数![]() 的图象记为
的图象记为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得
旋转180°得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得
旋转180°得![]() ,交
,交![]() 轴于点
轴于点![]() ;……如此进行下去,得到一条“波浪线”.若
;……如此进行下去,得到一条“波浪线”.若![]() 在这条“波浪线”上,则
在这条“波浪线”上,则![]() ____.
____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿OAB中,∠OAB=90°.OA=AB=6.将⊿OAB绕点O逆时针方向旋转90°得到⊿OA1B1
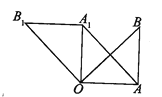
(1)线段A1B1的长是 ∠AOA1的度数是
(2)连结AA1,求证:四边形OAA1B1是平行四边形 ;
(3)求四边形OAA1B1的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
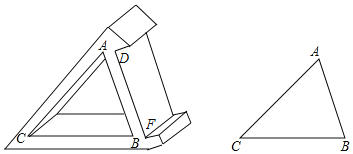
【题目】在全校的科技制作大赛中,王浩同学用木板制作了一个带有卡槽的三角形手机架.如图所示,卡槽的宽度DF与内三角形ABC的AB边长相等.已知AC=20cm,BC=18cm,∠ACB=50°,一块手机的最长边为17cm,王浩同学能否将此手机立放入卡槽内?请说明你的理由(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
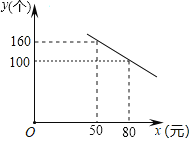
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,且抛物线与直线
,且抛物线与直线![]() 相交于
相交于![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .
.
(1)![]() ,
,![]() ,
,![]() (直接写出结果);
(直接写出结果);
(2)当![]() 时,则
时,则![]() 的取值范围为 (直接写出结果);
的取值范围为 (直接写出结果);
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使得
,使得![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 的最大面积及点
的最大面积及点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据:![]() ≈1.732,
≈1.732, ![]() ≈4.583,π≈3.142)
≈4.583,π≈3.142)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com