
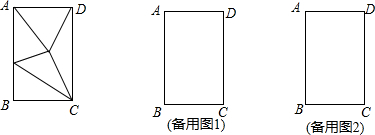
���� ��1�����۵������ʵõ��Ƴ���BCE�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2���������⻭��ͼ�μ��ɣ�
�ڸ���ȫ�������ε����ʵõ���PAC=��DCA����AP��CD�ཻ��O�����ǵõ�OA=OC����á�OAC=��OPD������ƽ���ߵ��ж������õ����ۣ�
��3����������������۵���������BE��ʾ��AE������ù��ɶ������ɣ�
��� �⣺��1������P��CD��ʱ����ͼ1��
�߽���B�����Ϸ����ۣ��ۺ�ΪCE��ʹ��B���ڵ�P����
���BCE=��ECP=45�㣬
���BCE�ǵ���ֱ�������Σ�
��BE=BC=AD=10��
����P�ھ����ڲ�ʱ��BE��ȡֵ��Χ��0��BE��10��
�ʴ�Ϊ��10��0��BE��10��
��2���ٲ�ȫͼ����ͼ2��ʾ��
�ڵ���E���A�غ�ʱ����ͼ3��
���۵��ã�AB=PC��
�ڡ�ADC���CPA�У�$\left\{\begin{array}{l}{AP=CD}\\{��ADC=��APC}\\{AC=AC}\end{array}\right.$��
���ADC�ա�CPA��
���PAC=��DCA��
��AP��CD�ཻ��O����OA=OC��
��OD=OP����ODP=��OPD��
�ߡ�AOC=��DOP��
���OAC=��OPD
��PD��AC��
��3������P����ֱ�ĶԳ�����ʱ���籸��ͼ1��
��CG=$\frac{1}{2}$BC=5��
���۵��ã�BE=PE��PC=BC=10��
��Rt��PCG�У����ݹ��ɶ����ã�PG=5$\sqrt{3}$��
����E��EF��PG��F��
��FG=BE����PF=PG-FG=5$\sqrt{3}$-BE��
��Rt��PEF�У����ݹ��ɶ����ã�BE2-��5$\sqrt{3}$-BE��2=25��
��BE=$\frac{10\sqrt{3}}{3}$��
����P��ˮƽ�ĶԳ�����ʱ���籸��ͼ2��
��BG=CH=$\frac{1}{2}$AB=8��
���۵�֪��PE=BE��PC=BC=10��
��Rt��CPH��PH=6��
��PG=4��
��Rt��PEG��EG=8-BE��PE=BE��
���ݹ��ɶ����ã�BE2-��8-BE��2=16
��BE=5��
��������������BE�ij�Ϊ5��$\frac{10\sqrt{3}}{3}$��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ�ȫ�������ε��ж������ʣ����������ε��ж������ʣ����ɶ����۵������ʣ�����ֱ�������ε����ʣ��߹���ͼ����ȷ�����������߹���ȫ���������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D��E�ֱ���AC��AB�ϵĵ㣬AC=7����EDC=60�㣬��ABC=120�㣬AE=BC��sinA=$\frac{3\sqrt{3}}{14}$�����ı���DEBC�����Ϊ$\frac{150\sqrt{3}}{49}$��
��ͼ���ڡ�ABC�У���D��E�ֱ���AC��AB�ϵĵ㣬AC=7����EDC=60�㣬��ABC=120�㣬AE=BC��sinA=$\frac{3\sqrt{3}}{14}$�����ı���DEBC�����Ϊ$\frac{150\sqrt{3}}{49}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{x-4}{x-1}$ | C�� | $\frac{2}{x-3}$ | D�� | $\frac{2}{x-1}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com