
【题目】(阅读材料)
小明同学遇到下列问题:
解方程组 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y,
这时原方程组化为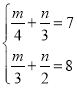 ,解得
,解得![]() ,
,
把![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得![]() 解得
解得![]() .
.
所以,原方程组的解为![]()
(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组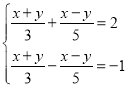 ;
;
(2)已知方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解.
的解.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115°
B.120°
C.130°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,A(1,0),C(0,2),双曲线y= ![]() (0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( )
(0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF , 则k值为( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )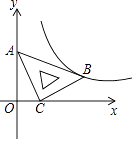
A.( ![]() ,0)
,0)
B.(2,0)
C.( ![]() ,0)
,0)
D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= ![]() (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ![]() ,则BN的长为 .
,则BN的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= ![]() x与y=
x与y= ![]() (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= ![]() x与y=
x与y= ![]() ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程:
(1)如图所示,设函数y= ![]() x与y=
x与y= ![]() 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则  ,
,
解得 ![]()
∴直线PA的解析式为 ![]()
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=ax2+bx+c ![]() 的图象如图所示,有以下四个结论:①abc=0,②
的图象如图所示,有以下四个结论:①abc=0,② ![]() ,③
,③ ![]() ,④
,④ ![]() ;其中正确的结论有( )
;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com