
【题目】如图,AB是⊙O直径,CD为⊙O的切线,C为切点,过A作CD的垂线,垂足为D.

(1)求证:AC平分∠BAD;
(2)若⊙O半径为5,CD=4,求AD的长.
【答案】(1)详见解析;(2)8;
【解析】
(1)连接OC,则OC⊥CD,因为CD⊥AD从而OC∥AD,利用平行线的性质及等边对等角,等量代换即可得到∠DAC=∠CAO,从而可知AC平分∠BAD
(2)过点O作OE⊥AD于点E,利用勾股定理求出AE,再利用![]() 即可求解.
即可求解.
(1)证明:如图1,连接OC,

∵直线CD切半圆O于点C,
∴OC⊥CD,
∵CD⊥AD,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∴AC平分∠BAD;
(2)如图2,过点O作OE⊥AD于点E,

∵∠OCD=∠OED=∠CDE=90°,
∴四边形OEDC是矩形,
∴DC=OE=4,
![]()
![]()


科目:初中数学 来源: 题型:
【题目】为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).
测试成绩(百分制)如下:
七年级:52,78,82,86,77,83,92,87,72,81,93,98,81,69,87,86,80,81,82,94
八年级:87,77,90,79,93,83,88,84,82,94,86,88,57,68,89,59,81,90,88,95
分组整理,描述数据
分组 | 七年级 | 八年级 | ||
画“正”计数 | 频数 | 画“正”计数 | 频数 | |
| 一 | 1 |
| 2 |
| 一 | 1 | 一 | 1 |
|
|
| 2 | |
|
| 正正 | 10 | |
|
| 4 | 正 | 5 |
七、八年级抽取学生的测试成绩统计表
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 82 |
| 81 | 20% |
八年级 | 82.5 | 86.5 |
| 25% |
根据以上信息,回答下列问题:
(1)表中![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]()
(2)若该校七年级270人和八年级280人参加了此次测试,估计参加此次测试成绩优秀的学生人数;
(3)根据以上数据,你认为该校七、八年级哪个年级学生掌握交通安全知识较好?并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快5G网络建设,某移动通信公司在一个坡度为2:1的山腰上建了一座5G信号通信塔AB,在距山脚C处水平距离39米的点D处测得通信塔底B处的仰角是35°,测得通信塔顶A处的仰角是49°,(参考数据:sin35°≈0.57,tan35°≈0.70,sin49°≈0.75,tan49°≈1.15),则通信塔AB的高度约为( )
A.27米B.31米C.48米D.52米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则△BCN的面积是( )
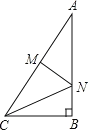
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.
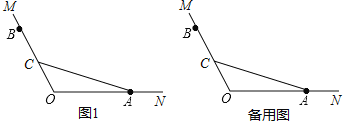
(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0
(1)若方程的一个根为 -1,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
(2)求证:不论![]() 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
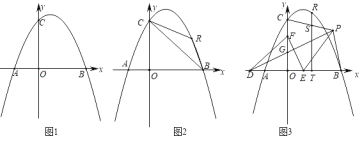
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com