

| A. | 2015π | B. | 3019.5π | C. | 3018π | D. | 3024π |
分析 首先求得每一次转动的路线的长,发现每4次循环,找到规律然后计算即可.
解答 解:转动一次A的路线长是:$\frac{90π×4}{180}$=2π,
转动第二次的路线长是:$\frac{90×π×5}{180}$=$\frac{5π}{2}$,
转动第三次的路线长是:$\frac{90×π×3}{180}$=$\frac{3π}{2}$,
转动第四次的路线长是:0,
转动五次A的路线长是:$\frac{90π×4}{180}$=2π,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为:$\frac{3π}{2}$+$\frac{5π}{2}$+2π=6π,
∵2016÷4=504
∴这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是:6π×504=3024π.
故选:D.
点评 本题主要考查了探索规律问题和弧长公式的运用.注意掌握旋转变换的性质、灵活运用弧长的计算公式、发现规律是解决问题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 6$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间(单位:秒)的关系图是( )| A. |  | B. | 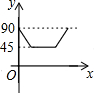 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com