

| A. | (4032,0) | B. | (4036,0) | C. | (8064,0) | D. | (8068,0) |
分析 由题意得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2017÷3=672…1,于是可判断三角形2017与三角形1的状态一样,然后计算672×12即可得到三角形2017的直角顶点坐标.
解答 解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∵AB=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2017÷3=672…1,
∴△2017的直角顶点是第671个循环组后第一个三角形的直角顶点,
∴三角形2017的直角顶点的横坐标=672×12=8064,
∴三角形2017的直角顶点坐标为(8064,0),
故选:C.
点评 此题考查了坐标与图形变化-旋转,仔细观察图形得到每三个三角形为一个循环组依次循环是解题的关键,也是求解的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
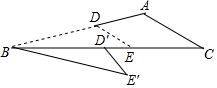 如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为2+$\sqrt{34}$.
如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为2+$\sqrt{34}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )
如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )| A. | (7,45) | B. | (8,44) | C. | (44,7) | D. | (45,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
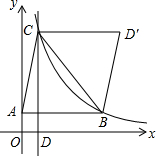 如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.
如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com