
分析 (1)把y=$\frac{ax+b}{cx+d}$变形,再由bc=ad,得出(cx+d)(cy-a)=0,根据分式有意义的条件,从而得出y是有理数;
(2)把y=$\frac{ax+b}{cx+d}$变形,再由bc≠ad,以及a,b,c,d都是有理数,x是无理数,得出y为无理数.
解答 解:(1)∵bc=ad,
∴b=$\frac{ad}{c}$,
∵y=$\frac{ax+b}{cx+d}$,
∴xcy+dy=ax+$\frac{ad}{c}$,
∴c2xy+cdy-acx-ad=0,
∴cx(cy-a)+d(cy-a)=0,
∴(cx+d)(cy-a)=0,
∵cx+d≠0(分母不为0),
∴cy-a=0,
∵a,c为有理数,
∴y为有理数;
(2)∵y=$\frac{ax+b}{cx+d}$,
∴xcy+dy=ax+b,
∴x=$\frac{b-dy}{cy-a}$,
∵x为无理数,a,b,c,d都是有理数,
∴y为无理数.
点评 本题考查了实数,以及它的分类,证明一个数是有理数或无理数是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | x2+3x-1=0 | C. | ax2+bx+c | D. | 3x+y=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
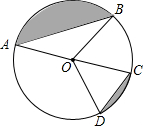 如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)
如图,A,B,C,D是⊙O上的四点,$\widehat{AB}+\widehat{CD}=\widehat{AD}+\widehat{BC}$,且AB=8,CD=4,则图中两个阴影部分的面积和是15.4.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com