
【题目】如图,直线y1=x+2与双曲线 ![]() 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.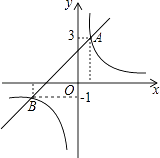
(1)求k的值;
(2)若y1<y2 , 请你根据图象确定x的取值范围.
【答案】
(1)解:把y=3代入y1=x+2得x=1,
把y=﹣1代入y1=x+2得x=﹣3,
∴A(1,3),B(﹣3,﹣1),
把A(1,3)代入 ![]() 得k=3
得k=3
(2)解:由图象知:当x<﹣3,或0<x<1时,y1<y2,
即若y1<y2,x的取值范围为:x<﹣3,或0<x<1
【解析】(1)由A、B在直线y1=x+2上,可求出A、B两点的坐标,再由待定系数法可求出反比例函数的解析式;
(2)结合图像可直接写出.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°= 0.53,cos32°= 0.85,tan32°= 0.62)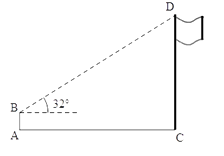
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小丽两位同学学习数学都养成了良好的预习习惯.某天他俩预习了课本第107页上的问题3,题目如下:
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
他俩都没有看课本上的解答过程,而是独立思考,分别列出了如下尚不完整的方程:
小明:![]() ; 小丽:
; 小丽:![]() .
.
(1)在小明、小丽所列的方程中,“□”中是运算符号,“( )”中是数字,试分别指出未知数![]() 、
、![]() 表示的意义;
表示的意义;
(2)试选择一种方法,将问题3解答完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA= ![]() ,依题意补全图形并求DE的长.
,依题意补全图形并求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P为∠ACB平分线上的一点,∠ACB=60°,PD⊥CA于D,PE⊥CB于E,点M是线段CP上的一动点(不与两端点C,P重合),连接DM,EM.
(1)求证:DM=EM;
(2)当点M运动到线段CP的什么位置时,四边形PDME为菱形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数 ![]() 的图象与性质.
的图象与性质.
小慧根据学习函数的经验,对函数 ![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数 ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)列出y与x的几组对应值.请直接写出m的值,m=;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系 ![]() , 描出以上表中各对对应值为坐标的点,并画出该函数的图象;
, 描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①;
② .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com