
已知二次函数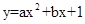 的图像过点(1,0)和(
的图像过点(1,0)和(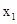 ,0),且
,0),且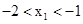 ,现在有5个判断:(1)
,现在有5个判断:(1)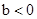 (2)
(2)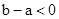 (3)
(3)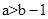 (4)
(4)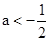 (5)
(5)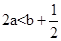 ,请把你认为判断正确的序号写出来 .
,请把你认为判断正确的序号写出来 .
(1)(3)(4)(5).
解析试题分析:如图,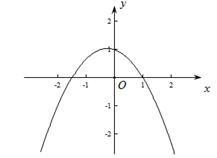
∵二次函数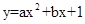 的图象经过点(x1,0)、(1,0),且﹣2<x1<﹣1,过(0,1),
的图象经过点(x1,0)、(1,0),且﹣2<x1<﹣1,过(0,1),
∴a<0,c>0,对称轴在y轴左侧,即x= <0,∴b<0,∴(1)正确;
<0,∴b<0,∴(1)正确;
∵二次函数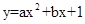 的图象经过点(x1,0)、(1,0),∴方程
的图象经过点(x1,0)、(1,0),∴方程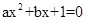 (a≠0)的两根为x1,1,∴1+x1=
(a≠0)的两根为x1,1,∴1+x1=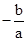 ,,而﹣2<x1<﹣1,∴﹣1<1+x1=
,,而﹣2<x1<﹣1,∴﹣1<1+x1=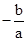 <0,∴
<0,∴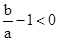 ,∵a<0,∴
,∵a<0,∴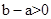 ,∴(2)错误.
,∴(2)错误.
∵由图象可知,当x=-1时,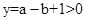 ,∴
,∴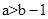 ,∴(3)正确;
,∴(3)正确;
∵二次函数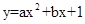 的图象经过点(x1,0)、(1,0),∴方程
的图象经过点(x1,0)、(1,0),∴方程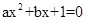 (a≠0)的两根为x1,1,∴x1=
(a≠0)的两根为x1,1,∴x1= ,即x1=
,即x1=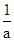 ,而﹣2<x1<﹣1,∴﹣2<
,而﹣2<x1<﹣1,∴﹣2<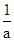 <﹣1,∵a<0,∴
<﹣1,∵a<0,∴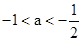 ,∴(4)正确.
,∴(4)正确.
由图象可知:对称轴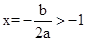 ,∴
,∴ ,∵a<0,∴
,∵a<0,∴ ,∴
,∴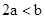 ,∴
,∴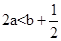 ,∴(5)正确.故答案为:(1)(3)(4)(5).
,∴(5)正确.故答案为:(1)(3)(4)(5).
考点:二次函数图象与系数的关系.


科目:初中数学 来源: 题型:填空题
如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 .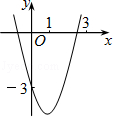
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
沙坪坝火车站将改造成一个集高铁、轻轨、公交、停车场、商业于一体的地下七层建筑,地面上欲建造一个圆形喷水池,如图, 点表示喷水池的水面中心,
点表示喷水池的水面中心,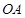 表示喷水柱子,水流从
表示喷水柱子,水流从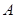 点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用
点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用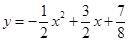 来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。
来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。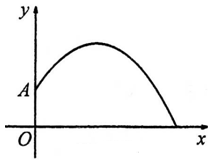
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线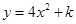 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数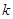 的取值范围是 .
的取值范围是 .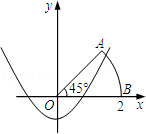
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 cm。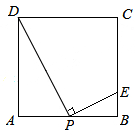
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com