【题目】如图，在直角坐标系中，点A，B分别在x，y轴上，点C是OB的中点，BE，CD都与x轴平行，BD⊥AB，∠ABO=30°．
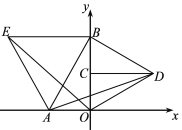
（1）判断△OBD的形状；
（2）若A（-3，0），BE=6，求证OE=AD．
【答案】（1）△OBD为等边三角形；（2）证明见详解
【解析】
（1）根据点C是OB的中点， CD与x轴平行得出
，通过BD⊥AB，∠ABO=30°，求出
60°，即可证明△OBD为等边三角形；（2）根据BE与x轴平行得出
=90°，由∠ABO=30°，∠AOB=90°推出AB=2OA=6，则可证明
，即可求证OE=AD．
解：（1）△OBD为等边三角形
在BOD中点C是OB的中点， CD与x轴平行
∴
又BD⊥AB，∠ABO=30°
∴60°
∴△OBD为等边三角形
（2）BE与x轴平行
∴BE⊥BO即=90°
又A（-3，0）
∴OA=3
又∠ABO=30°，∠AOB=90°
∴AB=2OA=6
∴AB=BE
在和中
∴
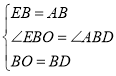
∴OE=AD
科目：初中数学 来源： 题型：
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正，他这天下午的行程记录如下：（单位：千米）
+15，-3，+14，-11，+10，-18，+14
（1）将最后一名乘客送到目的地时，小张离下午出车点的距离是多少？
（2）离开下午出发点最远时是多少千米？
（3）若汽车的耗油量为0.06升/千米，油价为4.5元/升，这天下午共需支付多少油钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠C=90°，斜边c=5，两直角边的长a，b是关于x的一元二次方程
的两个根，则Rt△ABC中较短的直角边长为__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，网格中有格点△ABC与△DEF．
（1）△ABC与△DEF是否全等？（不说理由．）
（2）△ABC与△DEF是否成轴对称？（不说理由．）
（3）若△ABC与△DEF成轴对称，请画出它的对称轴l．并在直线l上画出点P，使PA+PC最小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点D、F、E、G都在△ABC的边上，EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD的度数．（请在下面的空格处填写理由或数学式）
解：∵EF∥AD，（已知）
∴∠2＝ （ ）
∵∠1＝∠2，（已知）
∴∠1＝ （ ）
∴ ∥ ，（ ）
∴∠AGD+ ＝180°，（两直线平行，同旁内角互补）
∵∠BAC＝70°，（已知）
∴∠AGD＝ （等式性质）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）（﹣a3）2+a6＝_____．
（2）2a5b（﹣ab）3＝_____．
（3）
＝_____．
（4）（﹣a）3（﹣a）4＝_____．
（5）（x+2）（x﹣3）＝_____．
（6）（2×103）×（5×104）＝_____．（用科学记数法表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
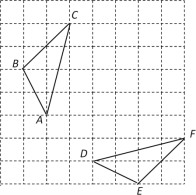
已知：等边三角形ABC
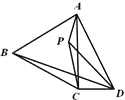
（1）如图1，P为等边△ABC外一点，且∠BPC=120°．试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想；
（2）如图2，P为等边△ABC内一点，且∠APD=120°．求证：PA+PD+PC＞BD
查看答案和解析>>
科目：初中数学 来源： 题型：
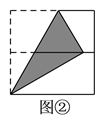
【题目】如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半，这样的图形有（ ）．
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
