
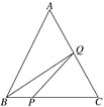
【题目】在△ABC中,已知AB=BC=CA=4 cm,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1 cm/s;点Q沿CA、AB向终点B运动,速度为2 cm/s,设它们运动的时间为x(s),当x=__________,△BPQ是直角三角形.
【答案】2或![]()
【解析】
用t表示出BP、CQ、BQ,然后分两种情况:①∠BPQ=90°,②∠BQP=90°进行讨论即可得解.
分析题意可知,只有点Q运动到AB上时,△BPQ才有可能是直角三角形,根据题意,得B、C两点运动的距离BP=tcm,CQ=2tcm, ∴BQ=(8-2t) cm,
若△BPQ是直角三角形,则∠BPQ=90°或∠BQP=90°,
①当∠BPQ=90°时,
Q在A点,CQ=CA=4 cm,
4÷2=2(s);
②当∠BQP=90°时,∵∠B=60°,
∴∠BPQ=90°-60°=30°,
∴BQ=![]() BP,
BP,
即8-2t=![]() t,
t,
解得t=![]() ,
,
故当t=2或![]() 秒时,△BPQ是直角三角形.
秒时,△BPQ是直角三角形.
故答案为:2或![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】直接写出结果:(1)-1+1=_____;(2)3-7=_____;
(3)4÷![]() =_____;(4)-7×0.5=_____;(5)(-2)3=_____;
=_____;(4)-7×0.5=_____;(5)(-2)3=_____;
(6)(-1)2n=_______(n为正整数);(7)4x=0的解是_____;
(8)![]() x=4 的解是_____.
x=4 的解是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有330台机器要运送到外地,计划租用甲、乙两种货车.已知甲种货车每辆租金400元,乙种货车每辆租金280元,若租用3辆甲种货车和2辆乙种货车,可运送195台机器;若租用4辆甲种货车和1辆乙种货车,可运送210台机器;
(1)求每辆甲种货车和乙种货车能运送的机器数量;
(2)请给出一次性将机器运送到目的地的最节省费用的租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )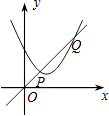
A.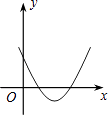
B.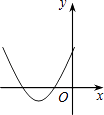
C.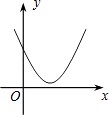
D.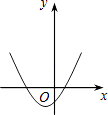
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 . 
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com