
【题目】如图,将一张正方形纸片![]() ,依次沿着折痕
,依次沿着折痕![]() ,
,![]() (其中
(其中![]() )向上翻折两次,形成“小船”的图样.若
)向上翻折两次,形成“小船”的图样.若![]() ,四边形
,四边形![]() 与
与![]() 的周长差为
的周长差为![]() ,则正方形
,则正方形![]() 的周长为______.
的周长为______.
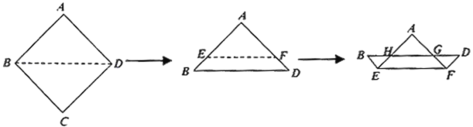
【答案】16
【解析】
由正方形的性质得出△ABD是等腰直角三角形,由EF∥BD,得出△AEF是等腰直角三角形,由折叠的性质得△AHG是等腰直角三角形,△BEH与△DFG是全等的等腰直角三角形,则GF=DF=BE=EH=1,设AB=x,则BD=![]() x,EF=
x,EF=![]() (x-1),AH=AG=x-2,HG=
(x-1),AH=AG=x-2,HG=![]() (x-2),由四边形BEFD与△AHG的周长差为5
(x-2),由四边形BEFD与△AHG的周长差为5![]() -2列出方程解得x=4,即可得出结果.
-2列出方程解得x=4,即可得出结果.
∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∵EF∥BD,
∴△AEF是等腰直角三角形,
由折叠的性质得:△AHG是等腰直角三角形,△BEH与△DFG是全等的等腰直角三角形,
∴GF=DF=BE=EH=1,
设AB=x,
则BD=![]() x,EF=
x,EF=![]() (x-1),AH=AG=x-2,HG=
(x-1),AH=AG=x-2,HG=![]() (x-2),
(x-2),
∵四边形BEFD与△AHG的周长差为5![]() -2,
-2,
∴![]() x+
x+![]() (x-1)+2-[2(x-2)+
(x-1)+2-[2(x-2)+![]() (x-2)]=5
(x-2)]=5![]() -2,
-2,
解得:x=4,
∴正方形ABCD的周长为:4×4=16,
故答案为:16.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
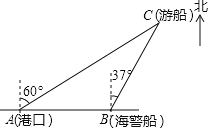
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一张等腰直角三角形板,
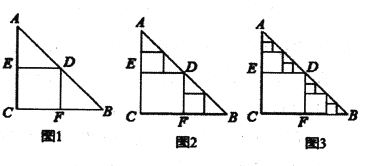
是一张等腰直角三角形板,![]() ,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第
,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第![]() 次剪取,记所得的正方形面积为
次剪取,记所得的正方形面积为![]() ;按照图1中的剪法,在余下的
;按照图1中的剪法,在余下的![]() 和
和![]() 中,分别剪取两个全等正方形,称为第
中,分别剪取两个全等正方形,称为第![]() 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为![]() ,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第
,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第![]() 次剪取,并记这四个正方形的面积和为
次剪取,并记这四个正方形的面积和为![]() ,(如图3);继续操作下去···则第
,(如图3);继续操作下去···则第![]() 次剪取后,
次剪取后,![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向左平移6个单位长度,得到点
向左平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有2个公共点时,求抛物线顶点横坐标
有2个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的出行方式,随机从全校2000名学生中抽取了300名学生进行调查,并根据调查结果绘制如下条形统计图,下列说法不正确的是( )
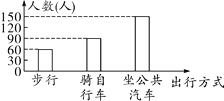
A.样本中步行人数最少
B.本次抽样的样本容量是300
C.样本中坐公共汽车的人数占调查人数的50%
D.全校步行、骑自行车的人数的总和与坐公共汽车的人数一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欢欢放学回家看到桌上有三个礼包,是爸爸送给欢欢和姐姐的礼物,其中![]() 礼包是芭比娃娃,
礼包是芭比娃娃,![]() 和
和![]() 礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
(1)欢欢随机地从桌上取出一个礼包,取出的是芭比娃娃的概率是多少?
(2)请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果,并求取出的两个礼包都是智能对话机器人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M![]() ,N
,N![]() ,给出如下定义:点M与点N的“折线距离”为:
,给出如下定义:点M与点N的“折线距离”为:![]()
![]()
![]() .
.

例如:若点M(-1,1),点N(2,-2),则点M与点N的“折线距离”为:![]() .根据以上定义,解决下列问题:
.根据以上定义,解决下列问题:
(1)已知点P(3,-2).
①若点A(-2,-1),则d(P,A)= ;
②若点B(b,2),且d(P,B)=5,则b= ;
③已知点C(m,n)是直线![]() 上的一个动点,且d(P,C)<3,求m的取值范围.
上的一个动点,且d(P,C)<3,求m的取值范围.
(2)⊙F的半径为1,圆心F的坐标为(0,t),若⊙F上存在点E,使d(E,O)=2,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
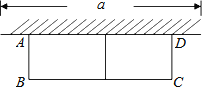
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大,最大面积为多少m2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com