
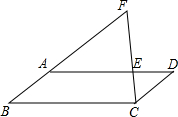
 如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小.
如图:E是平行四边形AD边上的一点,连接CE,并延长CE与BA的延长线交于点F,已知CE=ED,∠F=80°,求平行四边形各内角大小.  举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
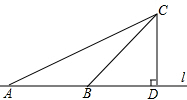 如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)
如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )| A. | 1:1:1 | B. | 1:2:3 | C. | 1:4:9 | D. | 1:3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
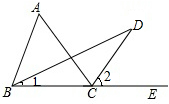 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com