
【题目】如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用)
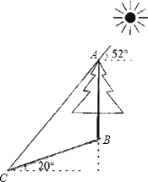
【答案】树高8.6米.
【解析】试题分析:过C作AB的垂线,设垂足为D.在Rt△CDB中,已知斜边BC=10m,利用三角函数求出CD和BD的长.同理在△ACD中,已知∠ACD=52°,CD,求出AD长,计算出AB=AD-BD,从而得到树的高度.
解:作CD⊥AB于D.
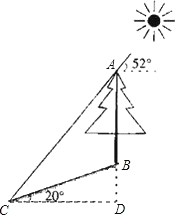
在Rt△BCD中,BC=10m,∠BCD=20°,
∴CD=BCcos20°≈10×0.940=9.40(m),
BD=BCsin20°≈10×0.342=3.42(m);
在Rt△ACD中,CD=9.40m,∠ACD=52°,
∴AD=CDtan52°≈9.40×1.280=12.032(m).
∴AB=AD-BD=12.032-3.42≈8.6(m).
答:树高8.6米.


科目:初中数学 来源: 题型:
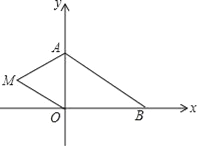
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.
(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣![]() 时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
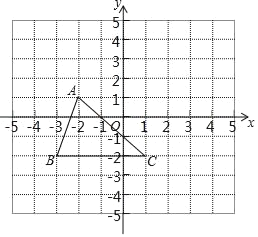
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'
(1)在图中画出△A′B′C';
(2)写出A',B'的坐标;
(3)求出△COC′的面积;
(4)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,垂足为D.
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校带领学生演出,参加演出的女生人数是男生人数的2倍少100人,学校需要采购一批演出服装.经了解:![]() 两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商:
两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商:![]() 公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费;
公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费;![]() 公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有
公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有![]() 人.
人.
(1)分别写出学校购买![]() 两公司服装所付的总费用
两公司服装所付的总费用![]() (元)和
(元)和![]() (元)与参演男生人数
(元)与参演男生人数![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)当参演男生人数是100人时,学校选用哪家制衣公司合算?当参演男生人数是300人时,学校选用哪家制衣公司合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)下表是y与x的几组对应值.m的值为_______;
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
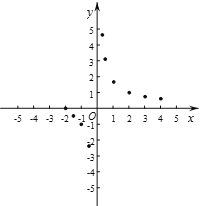
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:____________.
(5)结合函数图象估计![]() 的解的个数为_______个.
的解的个数为_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王勇和李华一起做风筝,选用细木棒做成如图所示的“筝形”框架,要求![]() ,
,![]() ,
,![]() .
.

(1)观察此图,是否是轴对称图形,若是,指出对称轴;
(2)![]() 和
和![]() 相等吗?为什么?
相等吗?为什么?
(3)判断![]() 是否被
是否被![]() 垂直平分,并说明你的理由.
垂直平分,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com