
����Ŀ���龳�۲죺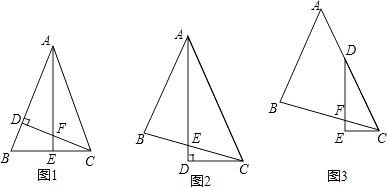
��1����ͼ1����ABC�У�AB=AC����BAC=45�㣬CD��AB��AE��BC������ֱ�ΪD��E��CD��AE���ڵ�F��
��д��ͼ1�����е�ȫ����������
���߶�AF���߶�CE��������ϵ�� ��
��2������̽����
��ͼ2����ABC�У���BAC=45�㣬AB=BC��ADƽ�֡�BAC��AD��CD������ΪD��AD��BC���ڵ�E��
��֤��AE=2CD��
��3����չ���죺
��ͼ3����ABC�У���BAC=45�㣬AB=BC����D��AC�ϣ���EDC= ![]() ��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
Ҫ������д�������ߵ�����������ͼ3�л��������ߣ�����Ҫ֤����
���𰸡�
��1����ABE�ա�ACE����ADF�ա�CDB��AF=2CE
��2���⣺֤�����ӳ�AB��CD���ڵ�G����ͼ2��ʾ��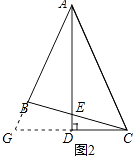
��ADƽ�֡�BAC��
���CAD=��GAD��
��AD��CD��
���ADC=��ADG=90�㣬
�ڡ�ADC�͡�ADG�У� ��
��
���ADC�ա�ADG��ASA����
��CD=GD����CG=2CD��
�ߡ�BAC=45�㣬AB=BC��
���ABC=90�㣬
���CBG=90�㣬
���G+��BCG=90�㣬
�ߡ�G+��BAE=90�㣬
���BAE=��BCG��
�ڡ�ABE�͡�CBG�У�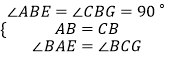 ��
��
���ABE�ա�CBG��ASA����
��AE=CG=2CD
��3���⣺��DG��BC��CE���ӳ�����G��
��ͼ3��ʾ��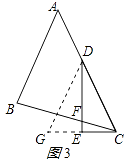
���������⣺��ͼ1�����е�ȫ��������Ϊ��ABE�ա�ACE����ADF�ա�CDB��
�ʴ�Ϊ����ABE�ա�ACE����ADF�ա�CDB
���߶�AF���߶�CE��������ϵ�ǣ�AF=2CE��
�ʴ�Ϊ��AF=2CE��
��1���ٸ��ݵ��������ε����ߺ�һ�ó�BE=CE,Ȼ������SSS�жϳ���ABE�ա�ACE����Rt��ADC�С�DAC=45�㣬�Ӷ��ó�AD=DC ,���ݵȽǵ������ȵó���DAF=��DCB ,�Ӷ�����ASA�жϳ���ADF�ա�CDB ������ȫ�������ζ�Ӧ����ȵó�AF=BC����CE=BE,�Ӷ��ó�AF=2CE ��
��2���ӳ�AB��CD���ڵ�G�����ݽ�ƽ���ߵĶ���ó���CAD=��GAD�����ݴ�ֱ�Ķ���ó���ADC=��ADG=90�㣬�Ӷ�����ASA�жϳ���ADC�ա�ADG ������ȫ�������ε����ʵó�CD=GD����CG=2CD �����ݵ��������ε����ʼ������ε��ڽǺ͵ó���ABC=90�� ����CBG=90�㣬����ͬ�ǵ������ȵó���BAE=��BCG���Ӷ�����ASA�жϳ���ABE�ա�CBG ���Ӷ��ó�AE=CG=2CD ��
��3����DG��BC��CE���ӳ�����G��ͬ��2��֤��������ȫ�ȣ��ó�DF=2CE ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������г��ȵ��߶�Ϊ�ߣ��ܹ���ֱ�������ε��ǣ� ��
A. 1��2��3 B. 3��4��5 C. 5��6��7 D. 7��8��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ϧ��͡Ϧ»�Ϊ��ǣ����Ϧ�=40�㣬��Ϧµ��ڣ�������
A. 40�� B. 50�� C. 60�� D. 140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
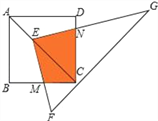
����Ŀ����ͼ����E��������ABCD�ĶԽ���AC�ϣ���EC=2AE��ֱ��������FEG����ֱ�DZ�EF��EG�ֱ�BC��DC�ڵ�M��N����������ABCD�ı߳�Ϊa�����ص������ı���EMCN�����Ϊ��������
A. ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a2
a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����ǿѧ�����ʣ�ȫ��ʵʩ��ѧ�������̡�Ӫ�����̣�ijƷ��ţ�̹�Ӧ���ṩ��ԭζ����ݮζ������ζ�����ζ������ζ���ֿ�ζ��ţ���ṩѧ�����ã������ѧΪ���˽�ѧ���Բ�ͬ��ζţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨ÿ�и��ֿ�ζţ�̵������ͬ������������ͼ���Ų�����������ͳ��ͼ��

��1�����α������ѧ������ ������
��2����ȫ���������ͳ��ͼ1���������ϲ�á�����ζ��ţ�̵�ѧ������������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3����У����1200��ѧ�������˸�Ʒ�Ƶ�ţ�̣�ţ�̹�Ӧ��ÿ��ֻΪÿ������ţ�̵�ѧ������һ��ţ�̣�Ҫʹѧ��ÿ�춼�ȵ��Լ�ϲ�õĿ�ζ��ţ�̣�ţ�̹�Ӧ��ÿ��������У��ţ���У���ݮζҪ��ԭζ���Ͷ��ٺУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
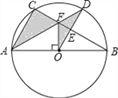
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AB�ǡ�O��ֱ����FO��AB������Ϊ��O������AF���ӳ�����O�ڵ�D������OD��BC�ڵ�E����B=30�㣬FO=2![]() ��
��
��1����AC�ij��ȣ�
��2����ͼ����Ӱ���ֵ���������������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=��x��1��2+4������ƽ��4����λ���ȣ�������ƽ��3����λ���ȣ��õ��������ߵĶ�������Ϊ�� ��
A.��5��4��
B.��1��4��
C.��1��1��
D.��5��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AC��BD�ཻ�ڵ�O��
��1����AB��4cm��AD��8cm����BC��cm��CD��cmʱ���ı���ABCDΪƽ���ı��Σ�
��2����BD��8cm��AC��10cm����AO��cm��DO��cmʱ���ı���ABCDΪƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� ��
A. ���������εױ��ϵ����߾��ǵױߵĴ�ֱƽ����
B. ���������εĶԳ����ǵױ��ϵĸ�
C. һ���߶οɿ����������Ĵ�ֱƽ����Ϊ�Գ������Գ�ͼ��
D. ���������εĶԳ�����Ƕ���ƽ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com