【题目】已知：如图，在菱形
中，对角线
、
相交于点
，
，
.
（1）求证：四边形
是矩形；
（2）若
，
，求四边形的面积.
【答案】（1）详见解析；（2）
.
【解析】
（1）根据平行四边形的判定定理得四边形AODE为平行四边形，再根据菱形的性质得出AC⊥BD，由矩形的判定定理得出四边形AODE是矩形；
（2）由矩形的性质，得出OA=DE=1．在Rt△AOB中，由勾股定理得出OB的长，由菱形的性质得出OD的长，即可求出四边形AODE的面积．
（1）∵DE∥AC，AE∥BD，∴四边形AODE是平行四边形．
∵四边形ABCD是菱形，∴AC⊥BD，∴∠AOD=90°，∴四边形AODE是矩形；
（2）∵四边形AODE是矩形，∴AO=DE=1．
∵AB=2，AC⊥BD，∴OB=
．
∵四边形ABCD是菱形，∴OD=OB，∴四边形AODE的面积=OAOD．
小学生10分钟口算测试100分系列答案科目：初中数学 来源： 题型：
【题目】下图为某区域部分交通线路图，其中直线
，直线
与直线
都垂直，，垂足分别为点A、点B和点C，（高速路右侧边缘），
上的点M位于点A的北偏东30°方向上，且BM＝
千米，
上的点N位于点M的北偏东
方向上，且
，MN=
千米，点A和点N是城际线L上的两个相邻的站点.
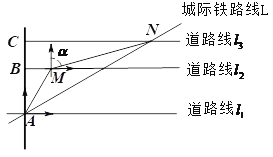
（1）求
之间的距离
（2）若城际火车平均时速为150千米/小时，求市民小强乘坐城际火车从站点A到站点N需要多少小时？（结果用分数表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，中线BE、CF相交于点G，连接EF，下列结论：
①
=
； ②
=； ③
=
； ④
=
．其中正确的个数有（ ）
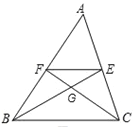
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x 轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2018个正方形的面积为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
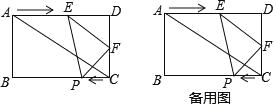
【题目】如图，在矩形 ABCD 中，AB＝6cm，AD＝8cm，直线 EF 从点 A 出发沿 AD 方向匀速运动，速度是 2cm/s，运动过程中始终保持 EF∥AC．F 交
AD 于 E，交 DC 于点 F；同时，点 P 从点 C 出发沿 CB 方向匀速运动，速度是 1cm/s，连接 PE、PF，设运动时间 t（s）（0＜t＜4）．
（1）当 t＝1 时，求 EF 长；
（2）求 t 为何值时，四边形 EPCD 为矩形；
（3）设△PEF 的面积为 S（cm2），求出面积 S 关于时间 t 的表达式；
（4）在运动过程中，是否存在某一时刻使 S△PC F：S 矩形 ABCD＝3：16？若存在， 求出 t 的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
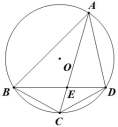
【题目】已知：如图，四边形 ABCD 内接于⊙ O ，AC 和 BD 相交于E ， BC = CD = 4 ， AE = 6 ，且 BE 和 DE 的长是正整数，求 BD 的 长．
查看答案和解析>>
科目：初中数学 来源： 题型：
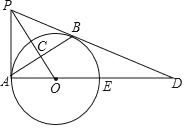
【题目】如图，PB与⊙O相切于点B，过点B作OP的垂线BA，垂足为C，交⊙O于点A，连结PA，AO，AO的延长线交⊙O于点E，与PB的延长线交于点D.
（1）求证：PA是⊙O的切线;
（2）若tan∠BAD=
， 且OC=4，求PB的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y＝ax2+bx+c（b≠0）的图象与x轴交于A、B两点，与y轴交于点C，点B坐标（﹣1，0），下面的四个结论：①OA＝3 ②a+b+c＜0 ③ac＞0 ④当y＞0时，﹣1＜x＜3，其中正确的结论是（ ）
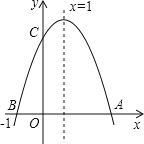
A.②④B.①③C.①④D.①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为
π，则图中阴影部分的面积为（ ）
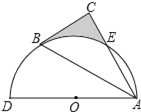
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com