
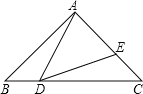
【题目】如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45度.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当:△ADE是等腰三角形时,求AE的长.
【答案】(1)见解析;(2)y=x2﹣![]() x+1.(3)AE的长为2﹣
x+1.(3)AE的长为2﹣![]() 或
或![]() .
.
【解析】
试题分析:此题有三问,(1)证明△ABD∽△DCE,已经有∠B=∠C,只需要再找一对角相等就可以了;
(2)由(1)证得△ABD∽△DCE,有相似就线段成比例,于是利用(1)的结果可证得(2);
(3)当△ABD∽△DCE时,可能是DA=DE,也可能是ED=EA,所以要分两种情况证明结论.
(1)证明:∵△ABC中,∠BAC=90°,AB=AC=1,
∴∠ABC=∠ACB=45°.
∵∠ADE=45°,
∴∠BDA+∠CDE=135°.
又∠BDA+∠BAD=135°,
∴∠BAD=∠CDE.
∴△ABD∽△DCE.
(2)解:∵△ABD∽△DCE,
∴![]() ;
;
∵BD=x,
∴CD=BC﹣BD=![]() ﹣x.
﹣x.
∴![]() ,
,
∴CE=![]() x﹣x2.
x﹣x2.
∴AE=AC﹣CE=1﹣(![]() x﹣x2)=x2﹣
x﹣x2)=x2﹣![]() x+1.
x+1.
即y=x2﹣![]() x+1.
x+1.
(3)解:∠DAE<∠BAC=90°,∠ADE=45°,
∴当△ADE是等腰三角形时,第一种可能是AD=DE.
又∵△ABD∽△DCE,
∴△ABD≌△DCE.
∴CD=AB=1.
∴BD=![]() ﹣1.
﹣1.
∵BD=CE,
∴AE=AC﹣CE=2﹣![]() .
.
当△ADE是等腰三角形时,第二种可能是ED=EA.
∵∠ADE=45°,
∴此时有∠DEA=90°.
即△ADE为等腰直角三角形.
∴AE=DE=![]() AC=
AC=![]() .
.
当AD=EA时,点D与点B重合,不合题意,所以舍去,
因此AE的长为2﹣![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,24,22,24,26,27,则这组数据的中位数与众数分别是( )
A. 23,24 B. 24,22 C. 24,24 D. 22,24
查看答案和解析>>
科目:初中数学 来源: 题型:
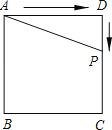
【题目】如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A.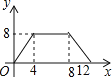 B.
B.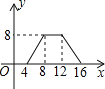 C.
C.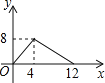 D.
D.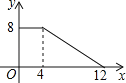
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地6月1日至6月7日每天最高、最低气温的折线统计图。
请你根据折线统计图,回答下列问题:
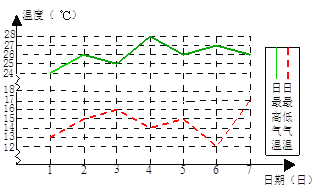
(1)在这7天中,日温差最大的一天是6月_____日;
(2)求这7天的日最高气温的平均数;
(3)求这7天日最高气温的方差。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
A. (-4,3) B. (-3,4) C. (4,-3) D. (3,-4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com