
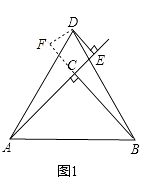
【题目】如图1,已知△ABC是等腰三角形,且∠ACB=90°,△ADB是等边三角形,点C在△ADB的内部,DE⊥AC交直线AC于点E. 
(1)你能证明“DE=CE”吗?试一试;
(2)如图2,若点C在△ADB的外部时,即点D、E在AB两侧,上述结论是否还成立?说明理由. 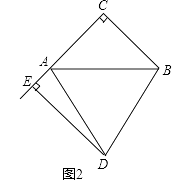
【答案】
(1)证明:如图1,过F作DF⊥BC,交BC延长线于F,则∠BFD=90°,
∵△ABD是等边三角形,
∴∠DAB=∠DBA=60°,AD=BD,
∵△ABC是等腰三角形,且∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠DAC=∠DBF=60°﹣45°=15°,
∵DE⊥AC,
∴∠AED=90°,
∴∠AED=∠BFD,
∴△ADE≌△BDF,
∴DF=DE,
∵∠BFD=∠AED=∠FCE=90°,
∴四边形DFCE是矩形,
∵DE=DF,
∴矩形DFCE是正方形,
∴DE=CE
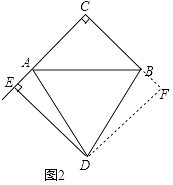
(2)证明:如图2,过D作DF⊥BC,交CB的延长线于F,则∠F=90°,
∵△ABD是等边三角形,
∴AD=BD,∠DAB=∠DBA=60°,
同理∠CAB=∠CBA=45°,
∴∠EAD=∠DBF=180°﹣60°﹣45°=75°,
∵∠AED=∠BFD=90°,
∴△AED≌△BFD,
∴DE=DF,
同理得:四边形DFCE是正方形,
∴DE=CE.
【解析】(1)如图1,作垂线,构建全等三角形,证明△ADE≌△BDF,得DF=DE,再证矩形DFCE是正方形,从而得出结论:DE=CE;(2)如图2,同理证明△AED≌△BFD和四边形DFCE是正方形,得出结论.
【考点精析】关于本题考查的等腰直角三角形和等边三角形的性质,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
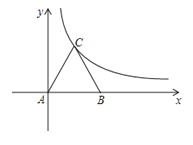
【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
 (1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽的说法正确吗?请说明理由;
(1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽的说法正确吗?请说明理由;
(2)请补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年5月18日华中旅游博览会在汉召开.开幕式上用到甲、乙、丙三种造型的花束,甲种花束由3朵红花、2朵黄花和1朵紫花搭配而成,乙种花束由2朵红花和2朵黄花搭配而成,丙种花束由2朵红花、1朵黄花和1朵紫花搭配而成.这些花束一共用了580朵红花,150朵紫花,则黄花一共用了________朵.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com