解:(1)3×30°+15°=105°.
∴钟面上2点30分时,钟面角为105°.
(2)2:00或10:00(答案不唯一)
(3)设经过x分钟,钟面角为35°,得:
6x+35=90+0.5x或者6x=90+0.5x+35
解得:x=10或x=
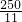
.
故在4点前,经过10或
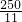
分钟,钟面角为35°
(4)60÷(1+

)
=60÷

=60×

=55

(分),
55

×

=

(分).
故小明是在12:

开始看电视的.
故答案为:105;2:00或10:00(答案不唯一);

.
分析:(1)钟表12个数字,每相邻两个数字之间的夹角为30°,钟表上2点30分,时针指向2和3的中间,分针指向6,两者之间相隔3.5个数字;
(2)找到时针和分针相隔2个数字的时刻即可;
(3)分两种情况,根据钟面角为35°讨论求解;
(4)当时针和分针正好交换位置时,时针和分针一共走了一圈.可根据路程问题进行解答,时针和分针两针所行的路程和是60个格子,分针每分钟走1小格,时钟每分钟走5÷60个格子.据此解答.
点评:考查了钟面角和一元一次方程的应用,(4)的关键是时针和分针正好交换位置时,两针共走了一圈,即60个格子,然后再根据路程问题进行解答.

 .
.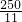 分钟,钟面角为35°
分钟,钟面角为35°  )
)

 (分),
(分), ×
× =
= (分).
(分).  开始看电视的.
开始看电视的. .
.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案