
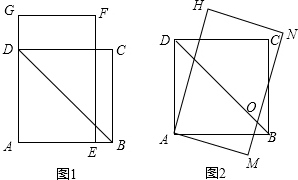
���� ��1������ת�����ʣ��ɵá�BAM=15�㣬���ɵá�OKB=��AOM=75�㣬���������ε����ʣ��ɵá�ABD=45�㣬Ȼ��������ǵ����ʣ�������á�DOM�Ķ�����
��2����������AM����BD��I������AN��������ǵ����Ǻ���ֵ����á�HAN=30�㣬������ת�����ʣ�������á�DAN=45�㣬����֤��A��C��N���ߣ�Ȼ���ɹɶ�����ô𰸣�
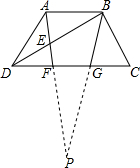
��3����Rt��ARK�У��������Ǻ����������AK��ֵ����AB�Ƚϴ�С������ȷ��B��λ�ã�
��� �⣺��1����������ã���BAM=15�㣬
���ı���AMNH�Ǿ��Σ�
���M=90�㣬
���AKM=90��-��BAM=75�㣬
���BKO=��AKM=75�㣬
���ı���ABCD�������Σ�
���ABD=45�㣬
���DOM=��BKO+��ABD=75��+45��=120�㣻
��2����ͼ2������AN����BD��I������DN��
��AE=72���ҡ�AFE=30�㣬
��EF=$\frac{7}{2}$$\sqrt{3}$��
��NH=$\frac{7}{2}$��AH=$\frac{7\sqrt{3}}{2}$����H=90�㣬
��tan��HAN=$\frac{NH}{AH}$=$\frac{\sqrt{3}}{3}$��
���HAN=30�㣬
��AN=2NH=7��
����ת�����ʣ���DAH=15�㣬
���DAN=45�㣬
�ߡ�DAC=45�㣬
��A��C��N���ߣ�
���ı���ABCD�������Σ�
��BD��AC��
��AD=CD=3$\sqrt{2}$��
��DI=AI=$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{A{B}^{2}+C{D}^{2}}$=3��
��NI=AN-AI=7-3=4��
��Rt��DIN��DN=$\sqrt{D{I}^{2}+N{I}^{2}}$=5��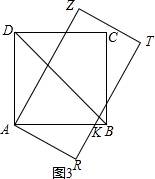
��3����B�ھ���ARTZ���ⲿ��
���ɣ���ͼ����������ã���BAR=15��+15��=30�㣬
�ߡ�R=90�㣬AR=$\frac{7}{2}$��
��AK=$\frac{AR}{cos30��}$=$\frac{\frac{7}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{7\sqrt{3}}{3}$��
��AB=3$\sqrt{2}$��$\frac{7\sqrt{3}}{3}$��
���B�ھ���ARTZ���ⲿ��
���� ���⿼������ת�����ʡ������ε����ʡ����ε����ʡ����ɶ����Լ�����ǵ����Ǻ������⣮�����ѶȽϴ�ע�����ν��˼���Ӧ�ã�ע��ȷ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
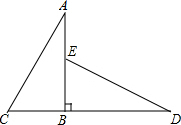
 ������ABCD�У�AB��CD����F��G���µ�CD�����ȷֵ㣬BG��AF���ӳ��߽��ڵ�P��AF��BD���ڵ�E����֤��PF•AE=PA•EF��
������ABCD�У�AB��CD����F��G���µ�CD�����ȷֵ㣬BG��AF���ӳ��߽��ڵ�P��AF��BD���ڵ�E����֤��PF•AE=PA•EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AB��CD������ΪB��AB=DB��AC=DE�������жϡ�D���A�Ĺ�ϵ����˵�����ɣ�
��ͼ����֪AB��CD������ΪB��AB=DB��AC=DE�������жϡ�D���A�Ĺ�ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
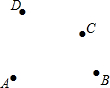 ��ͼ����֪A��B��C��D�ĸ��㣮
��ͼ����֪A��B��C��D�ĸ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2xy��2��ϵ����2 | B�� | ��ab��3�Ĵ�����6�� | ||
| C�� | $\frac{x+y}{5}$�ǵ���ʽ | D�� | x2-x�ij�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com