
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
分析 (1)描点、用平滑曲线连接这些点即可得出函数图象,观察函数图象猜测y是x的反比例函数,设y=$\frac{k}{x}$,代入点(3,20)即可求出k值,再将其余三点坐标代入其中验证后即可得出函数关系式;
(2)根据总利润=每本笔记本的利润×销售数量即可得出w关于x、y的函数关系式,将(1)得出的结论代入其内即可得出w与x之间的函数关系式;
(3)将x=8代入w=$\frac{60x-120}{x}$中即可求出结论.
解答 解:(1)依照题意,画出函数图象,如图所示.
猜测y是x的反比例函数,设y=$\frac{k}{x}$,
将点(3,20)代入y=$\frac{k}{x}$,
20=$\frac{k}{3}$,解得:k=60.
验证:把点(4,15)、(5,12)、(6,10)代入y=$\frac{60}{x}$都适合,
∴y是x的反比例函数,y=$\frac{60}{x}$(x>0).
(2)根据题意可知:w=(x-2)y,
∵y=$\frac{60}{x}$,
∴w=$\frac{60x-120}{x}$(x>0).
(3)当x=8时,w=$\frac{60x-120}{x}$=$\frac{60×8-120}{8}$=45.
∴当日销售单价为8元时,日销售利润是45元.
点评 本题考查了反比例函数的应用、待定系数法求函数解析式、以及代数式求值,解题的关键是:(1)利用待定系数法求出反比例函数关系式;(2)根据数量关系总利润=每本笔记本的利润×销售数量找出w关于x的函数关系式;(3)将x=8代入w=$\frac{60x-120}{x}$中求值.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
 CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.
已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
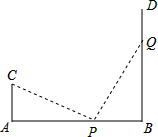 如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动3分钟后△CAP与△PQB全等.
如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动3分钟后△CAP与△PQB全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com