
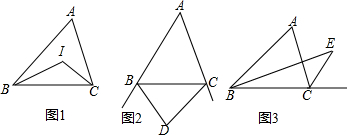
分析 (1)根据三角形的内角和定理以及角平分线的定义进行计算;
(2)根据三角形的内角和定理、角平分线的定义以及外角的性质进行计算即可;
(3)根据三角形的内角和定理、角平分线的定义以及外角的性质进行计算即可得出结论;
(4)根据平行线的性质以及邻补角的定义进行计算即可.
解答 解:(1)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∵点I是∠ABC,∠ACB的角平分线的交点,
∴∠IBC+∠ICB=65°,
∴△IBC中,∠BIC=180°-65°=115°;
(2)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∴∠ABC,∠ACB的外角之和=360°-130°=230°,
∵点D是∠ABC,∠ACB的外角平分线的交点,
∴∠DBC+∠DCB=115°,
∴△DBC中,∠BDC=180°-115°=65°;
(3)∠BEC=$\frac{1}{2}$∠BAC.
∵∠DCE是△BCE的外角,
∴∠E=∠DCE-∠CBE,
∵点E是∠ABC,∠ACG的平分线的交点,
∴∠DCE=$\frac{1}{2}$∠ACD,∠CBE=$\frac{1}{2}$∠ABC,
∴∠E=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A,
即∠BEC=$\frac{1}{2}$∠BAC;
(4)∵CE∥AB,
∴∠A=∠ACE=50°,
∵CE平分∠ACD,
∴∠ACD=100°,
∴∠ACB=180°-100=80°.
点评 本题主要考查了三角形的内角和定理、平行线的性质以及角平分线的定义的综合应用,解决问题的关键是掌握:三角形的内角和等于180°,三角形的外角等于与它不相邻的两个内角的和.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
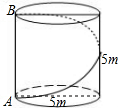 壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?
壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
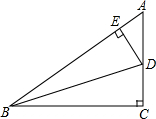 如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.
如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
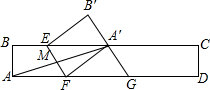 如图,在矩形ABCD中,AB=1,AD=6,F是AD上的点,且AF=2,E在BC上,沿EF折叠,使点A落在BC边上的点A′处,G是FD上的动点,连接AA′、A′G,当△AA′G为直角三角形时,AG的值为4或2+$\sqrt{3}$.
如图,在矩形ABCD中,AB=1,AD=6,F是AD上的点,且AF=2,E在BC上,沿EF折叠,使点A落在BC边上的点A′处,G是FD上的动点,连接AA′、A′G,当△AA′G为直角三角形时,AG的值为4或2+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.
如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①、② | B. | ①、③ | C. | ②、④ | D. | ③、④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com