
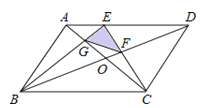
【题目】如图,平行四边形ABCD中,E是AD上的一点,且AE=![]() AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
【答案】C
【解析】试题分析:过A作AM⊥BC于M,如图所示: ∵S△BEC= ![]() BCAM,SABCD=BCAM,
BCAM,SABCD=BCAM,
∴S△BEC=![]() SABCD=
SABCD=![]() S, ∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,
S, ∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,
∴∠EAG=∠BCG,∠AEG=∠CBG, ∴△AEG∽△CBG,又AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() =
=![]() , ∴S△EFG=
, ∴S△EFG=![]() S△BGF, 又S△EFG+S△BGF=S△BEF,
S△BGF, 又S△EFG+S△BGF=S△BEF,
∴S△EFG=![]() S△BEF, ∵AE=
S△BEF, ∵AE=![]() AD,AD=AE+ED, ∴ED=
AD,AD=AE+ED, ∴ED=![]() AD=
AD=![]() BC,
BC,
同理得到△EFD∽△CFB, ∴![]() =
=![]() =
=![]() ∴S△BEF=
∴S△BEF=![]() S△BFC, 又S△BEF+S△BFC=S△BEC,
S△BFC, 又S△BEF+S△BFC=S△BEC,
∴S△BEF=![]() S△BEC=
S△BEC=![]() S, ∴S△EFG=
S, ∴S△EFG=![]() S.
S.



 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠C=90°,线段AD是△ABC的角平分线,直线DE是线段AB的垂直平分线.若DE=1cm,DB=2cm,AC= ![]() cm.求点C到直线AD的距离.
cm.求点C到直线AD的距离. 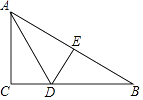
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1各顶点坐标;
(2)将△ABC向左平移1个单位,作出平移后的△A2B2C2 , 并写出△A2B2C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.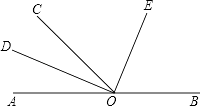
(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=5,AC=7,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB、AC相交于点M、N,且MN∥BC,则△AMN的周长等于 . 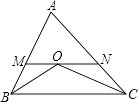
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把下面的频数分布表和频数分布直方图补充完整;
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 0.24 | |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | |
25<x≤30 | 2 | 0.04 |
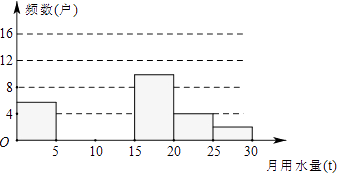
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为 . 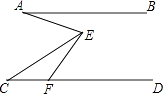
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式相乘的结果是a2﹣a﹣6的是( )
A.(a﹣2)(a+3)
B.(a+2)(a﹣3)
C.(a﹣6)(a+1)
D.(a+6)(a﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名画家达芬奇验证勾股定理的方法如下:
①在一张长方形的纸板上画两个边长分别为a、b的正方形,并连接BC、FE.
②沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ,请动手做一做.
③将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.
④比较两个多边形ABCDEF和A′B′C′D′E′F′的面积,你能验证勾股定理吗?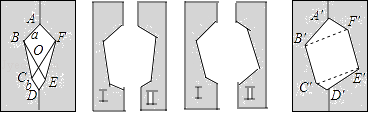
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com