
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)若点B是EF的中点,AB=![]() ,CB=
,CB=![]() ,求AE的长.
,求AE的长.

【答案】(1)见解析;(2)4![]() .
.
【解析】分析: (1)连接CD,由AC是⊙O的直径,可得出∠ADC=90°,由角的关系可得出∠EAC=90°,即得出EA是⊙O的切线;
(2)连接BC,由AC是⊙O的直径,可得出∠ABC=90°,由在RT△EAF中,B是EF的中点,可得出∠BAC=∠AFE,即可得出△EAF∽△CBA,利用相似从而求AE的长.
详解:
(1)∵弧AB=弧AB,∴∠D=∠C.
∵∠EAB=∠D,∴∠EAB=∠C.
∵AC是⊙O的直径,∴∠ABC=90°,
∴∠EAB+∠CAB=90°,
∴∠DAE=90°,
∴AE与⊙O相切;
(2)
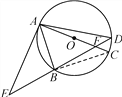
∵∠ABC=90°,AB=![]() ,CB=
,CB=![]() ,
,
∴AC=![]() =6,
=6,
由(1)知∠OAE=90°,
在Rt△EAF中,∵B是F的中点,
∴EF=2AB=![]()
∴∠BAF=∠BFA.
∵∠ABC=∠EAF,∴Rt△AFE∽Rt△BAC,
∴![]() ,
,![]() ,
,
AE=4![]() .
.
点睛: 本题主要考查了切线的判定和相似三角形的判定与性质,解题的关键是作出辅助线运用三角形相似及切线性质求解.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某超市按每袋20元的价格购进某种干果.销售过程中发现,每月销售量y(袋)与销售单价x(元)之间的关系可近似地看作一次函数:
![]() (
(![]() ).
).
(1)当x=45元时,y= 袋;当y=200袋时,x= 元;
(2)设这种干果每月获得的利润为w(元),当销售单价定为多少元时,每月 可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,直线y=![]() x-3与坐标轴交于A,B两点.
x-3与坐标轴交于A,B两点.
(1)求A,B两点的坐标;
(2)以AB为边在第四象限内作等边三角形ABC,求△ABC的面积;
(3)在平面内是否存在点M,使得以M,O,A,B为顶点的四边形是平行四边形,若存在,直接写出M点的坐标:若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知与填空:如图①,直线![]() ,求证:
,求证:![]() .
.
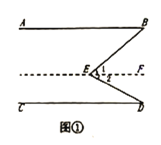
阅读下面的解答过程,并填上适当的理由,
解:过点![]() 作直线
作直线![]() ,
,
![]() ( )
( )
![]() (已知),
(已知),![]() ,
,
![]() ( )
( )
![]() ( )
( )
![]() ,
,
![]() ( )
( )
应用与拓展:如图②,直线![]() ,若
,若![]() .
.
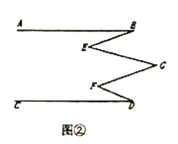
则![]() 度
度
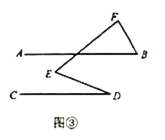
方法与实践:如图③,直线![]() ,若
,若![]() ,则
,则![]() 度.
度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P
(1) 求证:AP∥BC
(2) 若tan∠P=![]() ,求tan∠PAC的值
,求tan∠PAC的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一张长方形纸条上画一条数轴.

(1)若折叠纸条使数轴上表示﹣1的点与表示5的点重合,则折痕与数轴的交点表示的数是 ;
(2)如果数轴上两点之间的距离为6+m2(m为常数),这两点经过(1)的折叠方式后折痕与数轴的交点与(1)中的交点相同,求左边这个点表示的数;(用含m的代数式表示)
(3)如图2,若将此纸条沿A,B处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,求最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com