
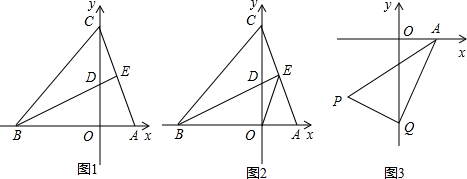
���� ��1���������C���꣬�ó���B���꣬���ֱ��AC����ʽ����BE��AC���ó�ֱ��BE����ʽ�����������D���ꣻ
��2���ɣ�1���ó�ֱ��AC��BE����ʽ��������ʾ��OF����ʽ�����������E��F�������$\frac{OF}{OE}$���ó���OEA�����ɣ�
��3�����жϳ���MPH=��NPQ���ó���PMH�ա�PNQ����PH=PQ�������жϳ���HPA�ա�QPA���õ���OAP=��PAQ=30�㼴�ɣ�
��� �⣺��1�����C��0��a����
��B��-a��0����
��A��1��0����
��ֱ��AC����ʽΪy=-ax+a��
��BE��AC��
����ֱ��BE�Ľ���ʽΪy=$\frac{1}{a}$x+b��
��B��-a��0����
��0=$\frac{1}{a}$����-a��+b��
��b=1��
��ֱ��BE�Ľ���ʽΪy=$\frac{1}{a}$x+1��
��D��0��1����
��2����OEC=135�㱣�ֲ��䣻
���ɣ���ͼ2��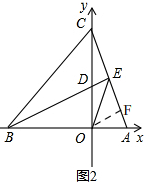
���C��0��a������B��-a��0����
����O��OF��AC��
��OF��BE��
�ɣ�1��֪��ֱ��AC����ʽΪy=-ax+a�٣�
ֱ��BE�Ľ���ʽΪy=$\frac{1}{a}$x+1�ڣ�
��ֱ��OF����ʽΪy=$\frac{1}{a}$x�ۣ�
�����٢ڵã�x=$\frac{a��a-1��}{{a}^{2}+1}$��y=$\frac{a��a+1��}{{a}^{2}+1}$��
��OE2=��$\frac{a��a-1��}{{a}^{2}+1}$��2+��$\frac{a��a+1��}{{a}^{2}+1}$��2=$\frac{2{a}^{2}��{a}^{2}+1��}{��{a}^{2}+1��^{2}}$��
�����٢۵ã�x=$\frac{{a}^{2}}{{a}^{2}+1}$��y=$\frac{a}{{a}^{2}+1}$��
��OF2=��$\frac{{a}^{2}}{{a}^{2}+1}$��2+��$\frac{a}{{a}^{2}+1}$��2=$\frac{{a}^{2}��{a}^{2}+1��}{��{a}^{2}+1��^{2}}$��
��$\frac{OF}{OE}=\frac{\sqrt{2}}{2}$��
��Rt��OEF��sin��OEF=$\frac{OF}{OE}=\frac{\sqrt{2}}{2}$��
���OEF=45�㣬
���OEC=135�㣻
������OEC=135�㱣�ֲ��䣻
��3����OQA�Ķ����Ƕ�ֵ��
���ɣ���ͼ3��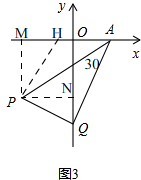
����P��PM��x�ᣬPN��y�ᣬPH��PQ��
�ߵ�PΪ��������ƽ������һ���㣬
��PM=PN��
�ߡ�MPH+��HPN=90�㣬��QPN+��HPN=90�㣬
���MPH=��NPQ��
�ڡ�PMH�͡�PNQ�У�$\left\{\begin{array}{l}{��MPJ=��NPQ}\\{PM=PN}\\{��PMH=��PNQ}\end{array}\right.$��
���PMH�ա�PNQ��
��PH=PQ��
��PH��PQ��
���HPA+��QPA=90�㣬
�ߡ�APQ=45�㣬
���HPA=45��=��QPA��
�ڡ�HPA�͡�QPA�У�$\left\{\begin{array}{l}{PH=PQ}\\{��HPA=��QPA=45��}\\{PA=PA}\end{array}\right.$��
���HPA�ա�QPA��
���PAH=��PAQ=30�㣬
���OQA=90��-��OAQ=90��-��PAQ-��OAP=30�㣬
������OQA�Ƕ�ֵΪ30�㣬
���� �����Ǽ��α任�ۺ��⣬��Ҫ�����˴���ϵ������ֱ�߽���ʽ��ֱ�ߵĽ������������ƽ���ߵ����ʶ�����ȫ�������ε��ж������ʣ��Ȿ��Ĺؼ��ǽ�ƽ���ߵ����ʶ�����Ӧ�ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ��С���� | C�� | ����ֵ��С���� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��-2 | D�� | x��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ھ������й�ѡ�� | B�� | �ھ���������ѡ�� | ||
| C�� | �ھ�����Ӣ��ѡ�� | D�� | �ھ�������������ѡ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com