
”¾ĢāÄæ”æĢ½Ė÷ÓėŌĖÓĆ£ŗ
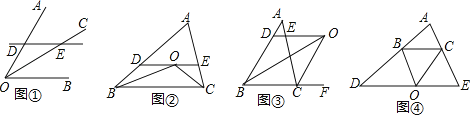
£Ø1£©»ł±¾Ķ¼ŠĪ£ŗČēĶ¼¢Ł£¬ŅŃÖŖOCŹĒ”ĻAOBµÄ½ĒĘ½·ÖĻߣ¬DE”ĪOB£¬·Ö±š½»OA”¢OCÓŚµćD”¢E£®ĒóÖ¤£ŗDE=OD£»
£Ø2£©ŌŚĶ¼¢ŚÖŠÕŅ³öÕāŃłµÄ»ł±¾Ķ¼ŠĪ£¬²¢ĄūÓĆ£Ø1£©ÖŠµÄ¹ęĀɽā¾öÕāøöĪŹĢā£ŗŅŃÖŖ”÷ABCÖŠ£¬Į½øöÄŚ½Ē”ĻABCÓė”ĻACBµÄĘ½·ÖĻß½»ÓŚµćO£¬¹żµćO×÷DE”ĪBC£¬½»AB”¢ACÓŚµćD”¢E£®ĒóÖ¤£ŗDE=BD+CE£»
£Ø3£©Čō½«Ķ¼¢ŚÖŠĮ½øöÄŚ½ĒµÄ½ĒĘ½·ÖĻßøÄĪŖŅ»øöÄŚ½Ē£ØČēĶ¼¢Ū£¬”ĻABC£©”¢Ņ»øöĶā½Ē£Ø”ĻACF£©ŗĶĮ½øö¶¼ŹĒĶā½Ē£ØČēĶ¼¢Ü”ĻDBC”¢”ĻBCE£©µÄ½ĒĘ½·ÖĻߣ¬ĘäĖüĢõ¼ž²»±ä£¬ŌņĻ߶ĪDE”¢BD”¢CEµÄŹżĮæ¹ŲĻµ·Ö±šŹĒ£ŗĶ¼¢ŪĪŖ ”¢Ķ¼¢ÜĪŖ £ŗ²¢“ÓÖŠČĪŃ”Ņ»øö½įĀŪÖ¤Ć÷£®
”¾“š°ø”æ£Ø1£©£Ø2£©£Ø3£©Ö¤Ć÷¼ū½āĪö
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾Ż½ĒĘ½·ÖĻߵĶØŅåµĆµ½”ĻAOC=”ĻBOC£¬øł¾ŻĘ½ŠŠĻߵĊŌÖŹµĆµ½”ĻDEO=”ĻBOC£¬µČĮæ“ś»»µĆµ½”ĻDEO=AOC£¬øł¾ŻµČŃüČż½ĒŠĪµÄÅŠ¶Ø¼“æɵƵ½½įĀŪ£»
£Ø2£©øł¾Ż”÷ABCÖŠ£¬”ĻABCŗĶ”ĻACBµÄĘ½·ÖĻßĻą½»ÓŚµćO£®ĒóÖ¤”ĻDBO=”ĻOBC£¬”ĻECO=”ĻBCO£¬ŌŁĄūÓĆĮ½Ö±ĻßĘ½ŠŠÄŚ“ķ½ĒĻąµČ£¬ĒóÖ¤³ö”ĻDOB=”ĻDBO£¬”ĻCOE=”ĻBCO£¬¼“BD=DO£¬OE=CE£¬Č»ŗóĄūÓƵČĮæ“ś»»¼“æÉĒó³ö½įĀŪ£»
£Ø3£©Ń”¢ŪÖ¤Ć÷£ŗÓÉ£Ø1£©ÖŠÖ¤Ć÷æÉµĆ£ŗDB=DO£¬EO=EC£¬øł¾ŻĻ߶ĪµÄŗĶ²ī¼“æɵƵ½½įĀŪ
Ö¤Ć÷£ŗ£Ø1£©”ßOCĘ½·Ö”ĻAOB£¬
”ą”ĻAOC=”ĻBOC£¬
”ßDE”ĪOB£¬
”ą”ĻDEO=”ĻBOC£¬
”ą”ĻDEO=AOC£¬
”ąDE=OD£»
£Ø2£©”ß”ĻABCŗĶ”ĻACBµÄĘ½·ÖĻßĻą½»ÓŚµćO£¬
”ą”ĻDBO=”ĻOBC£¬”ĻECO=”ĻBCO£¬
”ßDE”ĪBC£¬½»ABÓŚµćD£¬½»ACÓŚµćE£®
”ą”ĻDOB=”ĻDBO£¬”ĻCOE=”ĻECO£¬
”ąBD=DO£¬OE=CE£¬
”ąDE=BD+CE£»
£Ø3£©Ķ¼¢Ū£ŗDE=BD©CE£¬Ķ¼¢Ü£ŗDE=BD+CE£¬
Ń”¢ŪÖ¤Ć÷£ŗ
ÓÉ£Ø1£©ÖŠÖ¤Ć÷æÉµĆ£ŗDB=DO£¬EO=EC£¬
”ąDE=OD=OE=DB©CE£®
¹Ź“š°øĪŖ£ŗDE=BD©CE£¬DE=BD+CE£®


 Š”ѧ¶į¹ŚAB¾ķĻµĮŠ“š°ø
Š”ѧ¶į¹ŚAB¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£¬BµÄ×ų±ź·Ö±šĪŖA£Ø0£¬¦Į£©£¬B£Øb£¬¦Į£©£¬ĒŅ¦Į”¢bĀś×ć£Øa©2£©2+|b©4|=0£¬ĻÖĶ¬Ź±½«µćA£¬B·Ö±šĻņĻĀĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņ×óĘ½ŅĘ1øöµ„Ī»£¬·Ö±šµĆµ½µćA£¬BµÄ¶ŌÓ¦µćC£¬D£¬Į¬½ÓAC£¬BD£¬AB£®
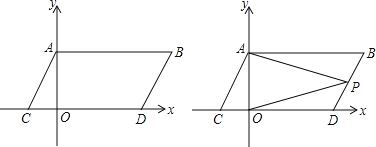
£Ø1£©ĒóµćC£¬DµÄ×ų±ź¼°ĖıߊĪABDCµÄĆ껿SĖıߊĪABCD
£Ø2£©ŌŚyÖįÉĻŹĒ·ń“ęŌŚŅ»µćM£¬Į¬½ÓMC£¬MD£¬Ź¹S”÷MCD=SĖıߊĪABDC£æČō“ęŌŚÕāŃłŅ»µć£¬Ēó³öµćMµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ŹŌĖµĆ÷ĄķÓÉ£®
£Ø3£©µćPŹĒĻ߶ĪBDÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓPA£¬PO£¬µ±µćPŌŚBDÉĻŅĘ¶ÆŹ±£Ø²»ÓėB£¬DÖŲŗĻ£©![]() µÄÖµŹĒ·ń·¢Éś±ä»Æ£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄÖµŹĒ·ń·¢Éś±ä»Æ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö¶ą±ßŠĪµÄĆæŅ»øöĶā½Ē¶¼µČÓŚ30”ć£¬ŌņÕāøö¶ą±ßŠĪµÄ±ßŹżŹĒ__£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅåŠĀŌĖĖć£ŗ¶ŌÓŚČĪŅāŹµŹża£¬b£¬¶¼ÓŠaØb=a£Øa©b£©+1£¬µČŹ½ÓŅ±ßŹĒĶس£µÄ¼Ó·Ø£¬¼õ·Ø¼°³Ė·ØŌĖĖć£®±ČČē£ŗ2Ø5=2”Į£Ø2©5£©+1=2”Į£Ø©3£©+1=©6+1=©5
£Ø1£©Ēó3أة2£©µÄÖµ£»
£Ø2£©Čō3ØxµÄÖµŠ”ÓŚ16£¬ĒóxµÄȔֵ·¶Ī§£¬²¢ŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
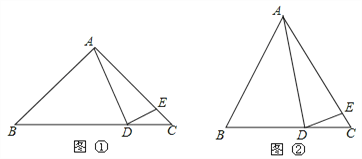
”¾ĢāÄæ”æ£Ø14·Ö£©Ģ½¾æÓė·¢ĻÖ£ŗČēĶ¼¢Ł£¬ŌŚRt”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AB=AC£¬µćDŌŚµ×±ßBCÉĻ£¬AE=AD£¬Į¬½įDE£®
£Ø1£©µ±”ĻBAD=60”揱£¬Ēó”ĻCDEµÄ¶ČŹż£»
£Ø2£©µ±µćDŌŚBC £ØµćB”¢C³żĶā£© ÉĻŌĖ¶ÆŹ±£¬ŹŌ²ĀĻė²¢Ģ½¾æ”ĻBADÓė”ĻCDEµÄŹżĮæ¹ŲĻµ£»
£Ø3£©ÉīČėĢ½¾æ£ŗČō”ĻBAC”Ł90”ć£¬ŹŌ¾ĶĶ¼¢ŚĢ½¾æ”ĻBADÓė”ĻCDEµÄŹżĮæ¹ŲĻµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌ²µÄĆ껿¹«Ź½ĪŖs=¦Šr2£¬ĘäÖŠ±äĮæŹĒ£Ø””””£©
A. s B. ¦Š C. r D. sŗĶr
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĻĀĮŠ½āĢā¹ż³ĢµÄæհד¦ĢīÉĻŹŹµ±µÄÄŚČŻ£ØĶĘĄķµÄĄķÓÉ»ņŹżŃ§±ķ“ļŹ½£©
ČēĶ¼£¬ŅŃÖŖAB”ĪCD£¬BE”¢CF·Ö±šĘ½·Ö”ĻABCŗĶ”ĻDCB£¬ĒóÖ¤£ŗBE”ĪCF£®
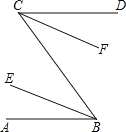
Ö¤Ć÷£ŗ
”ßAB”ĪCD£¬£ØŅŃÖŖ£©
”ą”Ļ =”Ļ £®£Ø £©
”ß £¬£ØŅŃÖŖ£©
”ą”ĻEBC=![]() ”ĻABC£¬£Ø½ĒµÄĘ½·ÖĻ߶ØŅ壩
”ĻABC£¬£Ø½ĒµÄĘ½·ÖĻ߶ØŅ壩
Ķ¬Ąķ£¬”ĻFCB= ![]() ”ĻBCD £®
”ĻBCD £®
”ą”ĻEBC=”ĻFCB£®£ØµČŹ½ŠŌÖŹ£©
”ąBE”ĪCF£®£Ø £©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĶ¬Ņ»Ö±½Ē×ų±źĻµÖŠ£¬ŗÆŹży=©![]() Óėy=ax+1£Øa”Ł0£©µÄĶ¼ĻóæÉÄÜŹĒ£Ø £©
Óėy=ax+1£Øa”Ł0£©µÄĶ¼ĻóæÉÄÜŹĒ£Ø £©
A£®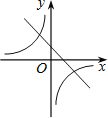 B£®
B£®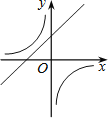 C£®
C£®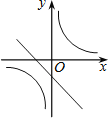 D£®
D£®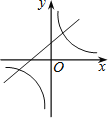
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com