
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
【答案】(1)需要甲车8辆,乙车10辆
(2)有三种运送方案:
①甲车型8辆,丙车型8辆;
②甲车型6辆,乙车型5辆,丙车型5辆;
③甲车型4辆,乙车型10辆,丙车型2辆;
(3)甲车型4辆,乙车型10辆,丙车型2辆时,最少运费是7800元.
【解析】
(1)设需要甲车![]() 辆,乙车
辆,乙车![]() 辆,根据运费
辆,根据运费![]() 元,总吨数120吨,列出方程组求解即可;
元,总吨数120吨,列出方程组求解即可;
(2)设甲车有![]() 辆,乙车有
辆,乙车有![]() 辆,丙车有
辆,丙车有![]() 辆,列出方程组,再根据
辆,列出方程组,再根据![]() 均为正整数,求出
均为正整数,求出![]() 的值,即可求解;
的值,即可求解;
(3)根据三种方案求出运费即可求解;
(1)设需要甲车![]() 辆,乙车
辆,乙车![]() 辆
辆
由题意可得:![]()
解得:![]()
![]() 需要甲车8辆,乙车10辆
需要甲车8辆,乙车10辆
(2)设甲车有![]() 辆,乙车有
辆,乙车有![]() 辆,丙车有
辆,丙车有![]() 辆
辆
由题意可得:![]()
消去![]() 可得:
可得:![]()
![]()
由于![]() 是非负整数,且不大于16,得:
是非负整数,且不大于16,得:![]()
由![]() 是非负整数,解得
是非负整数,解得
![]() 有三种运送方案:
有三种运送方案:
①甲车型8辆,丙车型8辆;
②甲车型6辆,乙车型5辆,丙车型5辆;
③甲车型4辆,乙车型10辆,丙车型2辆;
(3)三种方案得运费分别是:
①![]() ;
;
②![]() ;
;
③![]() .
.
![]() 甲车型4辆,乙车型10辆,丙车型2辆时,最少运费是7800元.
甲车型4辆,乙车型10辆,丙车型2辆时,最少运费是7800元.


科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)2a+3(a2-b)-2(2a2+a-![]() b),其中a=
b),其中a=![]() ,b=-2;
,b=-2;
(2)(m-5n+4mn)-2(2m-4n+6mn),其中m-n=4,mn=-3.
查看答案和解析>>
科目:初中数学 来源: 题型:
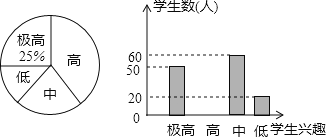
【题目】某中学为了了解学生参加体育运动的兴趣情况,从全校学生中随机抽取部分学生进行调查,对样本数据整理后画出如下统计图统计图不够完整请结合图中信息解答下列问题:
![]() 此样本的样本容量为:______;
此样本的样本容量为:______;
![]() 补全条形统计图;
补全条形统计图;
![]() 求兴趣为“中”的学生所占的百分比以及对应扇形的圆心角.
求兴趣为“中”的学生所占的百分比以及对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )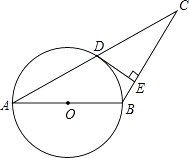
A.3
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.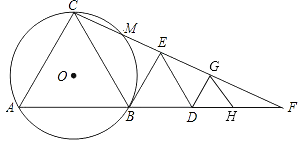
(1)求证:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.
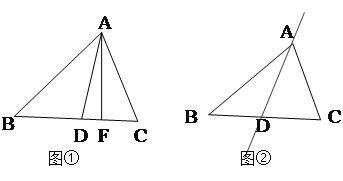
(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省教育厅下发了![]() 在全省中小学幼儿园广泛开展节约教育的通知
在全省中小学幼儿园广泛开展节约教育的通知![]() ,通知中要求各学校全面持续开展“光盘行动”
,通知中要求各学校全面持续开展“光盘行动”![]() 深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度
深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度![]() 程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”
程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”![]() ,对本市某所中学的学生进行了抽样调查
,对本市某所中学的学生进行了抽样调查![]() 我们将这次调查的结果绘制了以下两幅不完整统计图:
我们将这次调查的结果绘制了以下两幅不完整统计图:
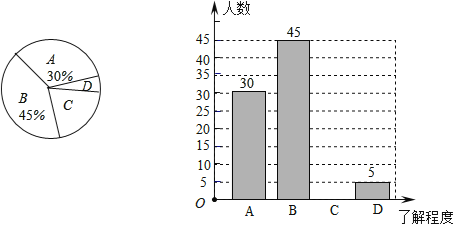
根据以上信息,解答下列问题:
![]() 补全条形统计图;
补全条形统计图;
![]() 本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
![]() 若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() ,宽为
,宽为![]() 的全等小矩形,且
的全等小矩形,且![]() .(以上长度单位:
.(以上长度单位:![]() )
)

(1)观察图形,发现代数式![]() 可以因式分解为_________________;
可以因式分解为_________________;
(2)若每块小矩形的面积为![]() ,四个正方形的面积和为
,四个正方形的面积和为![]() ,试求图中所有裁剪线(虚线部分)的长度之和.
,试求图中所有裁剪线(虚线部分)的长度之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com