
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.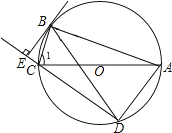
(1)求证:∠1=∠BAD;
(2)求证:BE是⊙O的切线.
【答案】
(1)
证明:∵BD=BA,
∴∠BDA=∠BAD,
∵∠1=∠BDA,
∴∠1=∠BAD;
(2)
证明:连接BO,
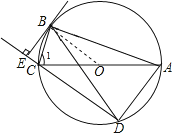
∵∠ABC=90°,
又∵∠BAD+∠BCD=180°,
∴∠BCO+∠BCD=180°,
∵OB=OC,
∴∠BCO=∠CBO,
∴∠CBO+∠BCD=180°,
∴OB∥DE,
∵BE⊥DE,
∴EB⊥OB,
∵OB是⊙O的半径,
∴BE是⊙O的切线.
【解析】(1)根据等腰三角形的性质和圆周角定理得出即可;(2)连接BO,求出OB∥DE,推出EB⊥OB,根据切线的判定得出即可;本题考查了三角形的外接圆与外心,等腰三角形的性质,切线的判定,熟练掌握切线的判定定理是解题的关键.
【考点精析】本题主要考查了圆周角定理和三角形的外接圆与外心的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( ) 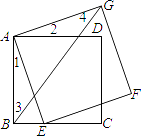
A.∠1<∠2
B.∠1>∠2
C.∠3<∠4
D.∠3>∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( ) 
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为cm.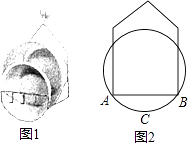
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A,B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,那个说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣1 | … |
(1)请在表内的空格中填入适当的数;
(2)请在所给的平面直角坐标系中画出y=x2﹣2x的图象;
(3)当x再什么范围内时,y随x的增大而减小;
(4)观察y=x2﹣2x的图象,当x在什么范围内时,y>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com