
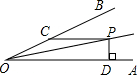
 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于D,PC=10,则PD=5.
如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于D,PC=10,则PD=5. 分析 过点P作PE⊥OB于E,根据角平分线的定义可得∠AOB=2∠AOP,根据两直线平行,同位角相等可得∠PCE=∠AOB,再根据直角三角形30°角所对的直角边等于斜边的一半可得PE=$\frac{1}{2}$PC,最后根据角平分线上的点到角的两边距离相等可得PD=PE.
解答 解:如图,过点P作PE⊥OB于E,
∵OP平分∠AOB,
∴∠AOB=2∠AOP=2×15°=30°,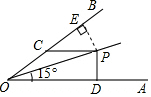
∵PC∥OA,
∴∠PCE=∠AOB=30°,
∴PE=$\frac{1}{2}$PC=$\frac{1}{2}$×10=5,
∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PD=PE=5.
故答案为:5.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质,熟记性质并作辅助线构造出直角三角形以及与PD相等的线段是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
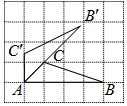 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚硬币,正面朝上 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | a是实数,|a|≥0 | |
| D. | 从车间刚生产的产品中任意抽取一件,是次品 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边形的内角和为360° | |
| B. | 一条对角线平分另一条对角线的四边形是平行四边形 | |
| C. | 四边都相等的四边形是菱形 | |
| D. | 矩形的四个角都是直角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com